Tabla de contenidos
Condición de nitidez de Gauss
Un espejo plano se forma para un objeto real, una imagen puntiaguda y nítida. Tal espejo es un sistema estigmático.
Un espejo esférico forma una imagen borrosa de un objeto puntual real. Tal espejo es un sistema astigmático.
El matemático, físico y astrónomo Gauss propuso dos condiciones para que las imágenes fueran relativamente nítidas en espejos esféricos. Son ellas:
– Los rayos de luz deben estar próximos al eje principal y ligeramente inclinados con relación a él. Tales rayos se llaman paraaxiales.
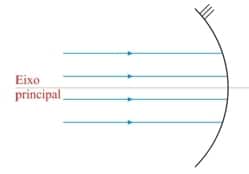
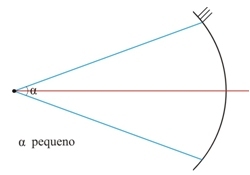
– El ángulo de apertura del espejo debe ser pequeño. En esta condición, el radio de curvatura del espejo debe ser grande, es decir, el espejo esférico se acerca al espejo plano.
Estudio analítico
El estudio analítico para obtener imágenes en espejos esféricos consiste en la determinación de estas imágenes a partir de cálculos. Cada procedimiento analítico será analizado en relación a un espejo esférico y rayos incidentes que obedecen a las condiciones de nitidez de Gauss.
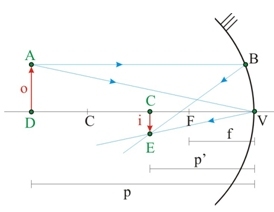
o → tamaño del objeto;
i → tamaño de la imagen;
f → distancia focal del espejo;
R → radio de curvatura del espejo;
p → posición del objeto en relación al vértice del espejo;
p ‘→ posición de la imagen en relación al vértice del espejo.
Entonces tenemos que:
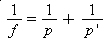
Incremento lineal transversal
La ampliación o ampliación de la imagen viene dada por:
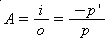
Sedo el foco del espejo aproximadamente igual al punto medio del centro de curvatura en el vértice del espejo, tenemos:
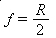
Convención de signos
- f> 0 → R> 0 → espejo cóncavo;
- f <0 → R <0 → espejo convexo;
- p> 0 → objeto real;
- p <0 → objeto virtual;
- p ‘> 0 → imagen real;
- p ‘<0 → imagen virtual;
- o> 0 → objeto hacia arriba;
- el objeto <0 → hacia abajo;
- i> 0 → imagen arriba;
- i <0 → imagen hacia abajo;
- A> 0 → imagen derecha en relación con el objeto;
- Una imagen <0 → invertida en relación con el objeto;
- | A | = 1 → imagen del mismo tamaño que el objeto;
- | A | > 1 → imagen más grande que el objeto;
- | A | <1 → imagen más pequeña que el objeto;