Tabla de contenidos
La distancia entre dos puntos es la medida del segmento de línea que los une.
Podemos calcular esta medida usando geometría analítica.
Distancia entre dos puntos en el plano
En el plano, un punto está completamente determinado conociendo un par ordenado (x, y) asociado con él.
Para conocer la distancia entre dos puntos, inicialmente los representaremos en el plano cartesiano, y luego calcularemos esta distancia.
Ejemplos:
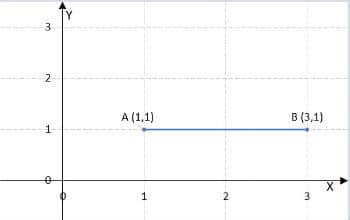
1) ¿Cuál es la distancia entre el punto A (1.1) y el punto B (3.1)?
d (A, B) = 3 – 1 = 2
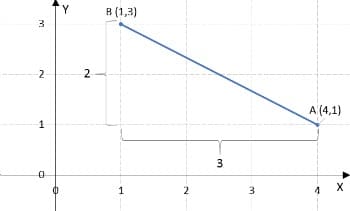
2) ¿Cuál es la distancia entre el punto A (4.1) y el punto B (1,3)?
Tenga en cuenta que la distancia entre el punto A y el punto B es igual a la hipotenusa del triángulo rectángulo con catetos 2 y 3.
Por lo tanto, usaremos el teorema de Pitágoras para calcular la distancia entre los puntos dados.
[d(A,B)]dos = 3dos + 2dos = √13
Fórmula de distancia entre dos puntos en el plano.
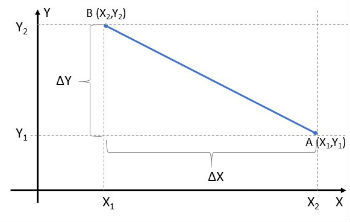
Para encontrar la fórmula de la distancia, podemos generalizar el cálculo realizado en el ejemplo 2.
Para dos puntos cualesquiera, como A (x1aa1) y B (xdosydos), tenemos:
Para obtener más información, lea también:
Distancia entre dos puntos en el espacio
Usamos un sistema de coordenadas tridimensional para representar puntos en el espacio.
Un punto está completamente determinado en el espacio cuando hay un triple ordenado (x, y, z) asociado a él.
Para encontrar la distancia entre dos puntos en el espacio, inicialmente podemos representarlos en el sistema de coordenadas y a partir de ahí, realizar los cálculos.
Ejemplo:
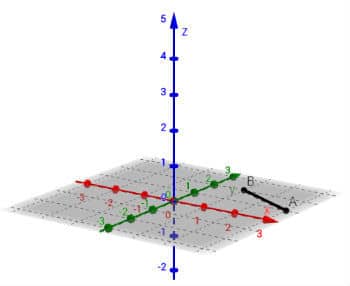
¿Cuál es la distancia entre el punto A (3,1.0) y el punto B (1,2.0)?
En este ejemplo, vemos que los puntos A y B pertenecen al plano xy.
La distancia vendrá dada por:
[d(A,B)]dos = 1dos + 2dos = √5
Fórmula de distancia entre dos puntos en el espacio.
Para obtener más información, lea también:
Ejercicios resueltos
1) Un punto A pertenece al eje de abscisas (eje x) y es equidistante de los puntos B (3.2) y C (-3.4). ¿Cuáles son las coordenadas del punto A?
2) La distancia del punto A (3, a) al punto B (0.2) es igual a 3. Calcule el valor de la ordenada a.
3) ENEM – 2013
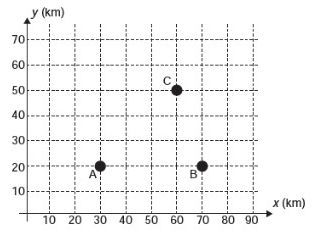
En los últimos años, la televisión ha experimentado una auténtica revolución, en cuanto a calidad de imagen, sonido e interactividad con el espectador. Esta transformación se debe a la conversión de la señal analógica a la señal digital. Sin embargo, muchas ciudades aún no cuentan con esta nueva tecnología. Buscando llevar estos beneficios a tres ciudades, una estación de televisión pretende construir una nueva torre de transmisión, que envía una señal a las antenas A, B y C, que ya existen en estas ciudades. Las ubicaciones de las antenas se representan en el plano cartesiano:
La torre debe estar ubicada en una ubicación equidistante de las tres antenas. El lugar adecuado para la construcción de esta torre corresponde al punto de coordenadas
a) (65; 35)
b) (53; 30)
c) (45; 35)
d) (50; 20)
e) (50; 30)
Ver también: ejercicios de distancia entre dos puntos
4) ENEM – 2011
Se planificó un barrio de una ciudad en una región plana, con calles paralelas y perpendiculares, delimitando manzanas del mismo tamaño. En el siguiente plano cartesiano de coordenadas, esta vecindad se ubica en el segundo cuadrante, y las distancias en el
los ejes se expresan en kilómetros.
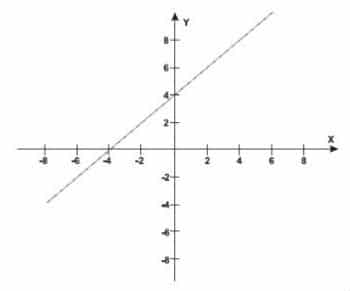
La recta de la ecuación y = x + 4 representa la planificación del recorrido de la línea del metro subterráneo que cruzará el barrio y otras regiones de la ciudad.
En el punto P = (-5,5), se ubica un hospital público. La comunidad solicitó al comité de planificación que planificara una estación de metro para que su distancia al hospital, medida en línea recta, no supere los 5 km.
En respuesta a la solicitud de la comunidad, el comité argumentó correctamente que esto se cumpliría automáticamente, ya que la construcción de una estación en el punto ya estaba prevista.
a) (-5,0)
b) (-3,1)
c) (-2,1)
d) (0,4)
e) (2,6)
Ver también: Ejercicios de geometría analítica