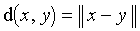espacio vectorial –

Generalización de espacios vectoriales de geometría.

MATEMÁTICAS

Espacio vectorial

La estructura del espacio vectorial sobre un campo K es una de las nociones básicas del álgebra lineal. En geometría, un espacio afín se define a partir de un espacio vectorial, cualquier estudio en el espacio afín se reduce a un estudio en el espacio vectorial asociado. El estudio de espacios vectoriales cuyos elementos son funciones, dotados de una normativa adecuada, se ha convertido en uno de los elementos esenciales del análisis. Los principales ejemplos de espacios vectoriales son los conjuntos formados por los siguientes elementos: polinomios con uno indeterminado, matrices de tipo (n, p) en un campo K; los mapas lineales del espacio de vector K E en el espacio de vector K F, las formas lineales de un espacio de vector K E.

Cualquier espacio K-vector E admite al menos dos subespacios vectoriales, el singleton {0} y E mismo. El conjunto de todas las combinaciones lineales finitas de elementos de una parte A de E es un subespacio vectorial de E. El subespacio vectorial F generado por no elementos X₁, X₂,…, X_node E es el subespacio vectorial de combinaciones lineales de X₁, X₂,…, X_no ; dicen que X₁, X₂,…, X_noes una parte generadora de F. Si el propio espacio E es generado por un número finito de sus elementos, se dice que es de dimensión finita.

El estudio de mapas lineales entre dos espacios vectoriales de dimensión finita desde su base conduce al cálculo matricial, el de la noción de forma multilineal a la teoría de determinantes y el de formas lineales de un espacio vectorial a las nociones de dual y tensor.

Espacio vectorial de dimensión finita

Un espacio vectorial de dimensión finita es un espacio vectorial generado por un número finito de sus elementos.

Cualquier subespacio vectorial de E también es de dimensión finita o igual a la de E. Si F es un mapa lineal de un espacio de K-vector E en un espacio de K-vector F, entonces la dimensión de F(MI) es finito y menor o igual al de E; define el rango de F y

rgF) = dim E – dim ker (F),

kerF) denotando el núcleo de F. En el caso de que E y F tengan la misma dimensión, las siguientes propiedades son equivalentes: F es biyectiva, F es inyectable y F es sobreyectiva.

Doble de un espacio K-vector E

Juntos ℒ (E; K) formas lineales definidas de E a K. (las denotamos por E *.)

Si E es de dimensión finita no, y si
es de base E, entonces mi^*es también de dimensión finita no. Una base de mi^*es
o Para_I* es definido por

, con
.

Estándar

Sobre el conjunto ℝ de reales como espacio vectorial, el mapa que, a cualquier real, asocia su valor absoluto es una norma. Sobre el conjunto ℂ de los complejos, la aplicación que, con cualquier complejo, asocia su módulo es un estándar. Cualquier espacio provisto de un estándar puede ser provisto con una distancia, más particularmente la distancia definida por
.