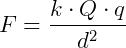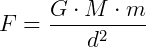Tabla de contenidos
La fuerza eléctrica es la interacción de atracción o repulsión generada entre dos cargas debido a la existencia de un campo eléctrico a su alrededor.
La capacidad de una carga para crear fuerzas eléctricas fue descubierta y estudiada por el físico francés Charles Augustin de Coulomb (1736-1806) a finales del siglo XVIII.
Hacia 1780, Coulomb creó el balance de torsión y con este instrumento demostró experimentalmente que la intensidad de la fuerza eléctrica es directamente proporcional al valor de las cargas eléctricas que interactúan e inversamente proporcional al cuadrado de la distancia que las separa.
Fórmula de fuerza eléctrica
La fórmula matemática, también llamada Ley de Coulomb, que expresa la intensidad de la fuerza eléctrica es:
En el Sistema Internacional de Unidades (SI), la intensidad de la fuerza eléctrica (F) se expresa en newton (N).
Los términos que1 eqdos de la fórmula corresponden a los valores absolutos de las cargas eléctricas, cuya unidad SI es el culombio (C), y la distancia que separa las dos cargas (r) se representa en metros (m).
La constante de proporcionalidad (K) depende del medio en el que se insertan las cargas, por ejemplo, en el vacío este término se llama constante electrostática (K0) y su valor es 9,109 Nodos/Cdos.
Aprender más sobre Ley de Coulomb.
¿Para qué se utiliza la fórmula de la fuerza eléctrica y cómo calcularla?
La fórmula creada por Coulomb se utiliza para describir la intensidad de la interacción mutua entre dos cargas puntuales. Estas cargas son cuerpos electrificados cuyas dimensiones son insignificantes en comparación con la distancia entre ellos.
La atracción eléctrica se produce entre cargas que tienen signos opuestos, porque la fuerza existente es la de atracción. La repulsión eléctrica ocurre cuando se juntan cargas del mismo signo, ya que la fuerza repulsiva actúa sobre ellas.
Para calcular la fuerza eléctrica no se tienen en cuenta los signos de las cargas eléctricas, solo sus valores. Vea cómo calcular la fuerza eléctrica con los siguientes ejemplos.
Ejemplo 1: Dos partículas electrificadas, q1 = 3,0 x 10-6 C eqdos = 5,0 x 10-6 C, y de dimensiones insignificantes están situadas a una distancia de 5 cm entre sí. Determine la fuerza de la fuerza eléctrica considerando que están en el vacío. Utilice la constante electrostática K0 = 9. 109 Nodos/Cdos.
Solución: Para encontrar la fuerza eléctrica, los datos deben aplicarse en la fórmula con las mismas unidades que la constante electrostática.
Tenga en cuenta que la distancia se dio en centímetros, pero la constante es metro, por lo que el primer paso es transformar la unidad de distancia.
El siguiente paso es reemplazar los valores en la fórmula y calcular la fuerza eléctrica.
Llegamos a la conclusión de que la intensidad de la fuerza eléctrica que actúa sobre las cargas es de 54 N.
Usted también podría estar interesado en Electrostática.
Ejemplo 2: La distancia entre los puntos A y B es de 0,4 my las cargas Q se encuentran en los extremos1 y Qdos. Un tercer cargo, Q3, se insertó en un punto que está a 0,1 m de Q1.
Calcule la fuerza neta sobre Q3 Sabiendo que:
- Q1 = 2,0 x 10-6 C
- Qdos = 8,0 x 10-6 C
- Q3 = – 3,0 x 10-6 C
- K0 = 9. 109 Nodos/Cdos
Solución: El primer paso para resolver este ejemplo es calcular la fuerza de la fuerza eléctrica entre dos cargas a la vez.
Comencemos calculando la fuerza de atracción entre Q1 y Q3.
Ahora, calculamos la fuerza de atracción entre Q3 y Qdos.
Si la distancia total entre la línea es de 0,4 my Q3 se coloca a 0,1 m de A, lo que significa que la distancia entre Q3 y Qdos es de 0,3 m.
A partir de los valores de las fuerzas de atracción entre las cargas, podemos calcular la fuerza resultante de la siguiente manera:
Llegamos a la conclusión de que la fuerza eléctrica resultante que Q1 y Qdos ejercer sobre Q3 es 3 N.
Fuerza eléctrica y Electromagnetismo
Siempre cuando se habla de fuerza eléctrica, se hace una comparación con la fuerza gravitacional, ya que ambas se describen de forma análoga: dos cuerpos que interactúan debido a una fuerza, que disminuye cuando los cuerpos se separan, o aumenta cuando los cuerpos se juntan. Un ejemplo de esto, en fuerza eléctrica, se ve al pasar un peine de látex por el cabello y tratar de acercarse a pequeños trozos de papel. Habrá una atracción, pero si no te acercas lo suficiente, no funcionará. Existe tal similitud entre las fuerzas eléctricas y gravitacionales que incluso las ecuaciones que gobiernan estas dos fuerzas son idénticas, veremos más adelante.
Sin embargo, existen dos diferencias entre las fuerzas eléctricas y gravitacionales:
- La primera diferencia es que la fuerza eléctrica puede unir o repeler los dos o más cuerpos que interactúan, mientras que la fuerza gravitacional solo los atraerá.
- La segunda diferencia es que la fuerza eléctrica es mucho más intensa que la fuerza gravitacional.
Afortunadamente, existen estas diferencias, porque si no hubiera equilibrio entre la atracción y la repulsión de la fuerza eléctrica, o el Universo sería comprimido por la atracción muy fuerte, convirtiéndose en una esfera compacta, o experimentaría una gran expansión, convirtiéndose en una nube gaseosa, debido a la repulsión. Y todo esto porque la fuerza eléctrica predomina sobre la gravitacional en lo que a intensidad se refiere.
Este equilibrio entre las fuerzas de atracción y repulsión se debe al hecho de que hay el mismo número de partículas positivas y negativas en un todo.
En el estudio de la física, la fuerza eléctrica se incluye en el contenido de la electrostática, una rama de la física que estudia las cargas eléctricas en reposo (detenidas), en relación con una referencia inercial.
La fuerza eléctrica hace que las cargas eléctricas del mismo signo (tanto positivas como negativas) se repelan y las señales opuestas se atraigan entre sí (positivas y negativas). Como los tamaños de estas cargas son extremadamente menores en relación con la distancia entre ellos, se consideran cuerpos puntuales y se denominan cargas puntuales.
Después de Joseph Priestley (1733-1804), responsable del descubrimiento del elemento oxígeno, infiriendo teorías y repitiendo los experimentos de Benjamin Franklin (1706-1790), hacia 1766, sobre la ley de las fuerzas, encontrando relaciones entre eléctrica y gravitacionalmente, la La ecuación de la fuerza eléctrica se definió directamente en 1785, cuando Charles Augustin de Coulomb (1736-1806) utilizó el balance de torsión para determinarla. Posteriormente, este balance de torsión se utilizó para medir la constante gravitacional (G).
La ecuación de la fuerza eléctrica se conoció como Ley de Coulomb y viene dada por
Donde
- F es la fuerza eléctrica de atracción o repulsión entre las cargas Q y q;
- d es la distancia entre las cargas Q y q;
- k es la constante electrostática.
Al calcular esta fuerza en el vacío, la constante k se convierte en k0 y viene dado por el valor:
k0 = 8,98755. 109 No. m² / C²
De esta forma, la fuerza eléctrica, matemáticamente, se define por el producto de las cargas eléctricas dividido por el cuadrado de la distancia entre ellas, así como la fuerza gravitacional, que es proporcional al producto de las masas e inversamente proporcional a la cuadrado de la distancia entre ellos,
Priestley había predicho esta similitud entre las ecuaciones.