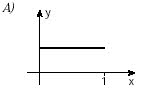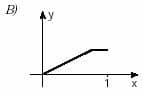Tabla de contenidos
Una función de inyector, también llamada función inyectiva, es un tipo de función que tiene elementos correspondientes en otra.
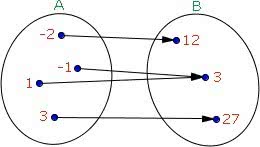
Así, dada una función f (f: A → B), todos los elementos del primero tienen como imagen elementos diferentes de B. Sin embargo, no hay dos elementos diferentes de A con la misma imagen de B.
Además de la función de inyección, tenemos:
Función Overjet: cada elemento del contradominio de una función es la imagen de al menos un elemento del dominio de otro.
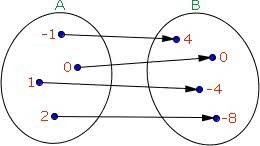
Función de biyector: es una función inyectora y sobreyectiva, donde todos los elementos de una función corresponden a todos los elementos de otra.
Ejemplo
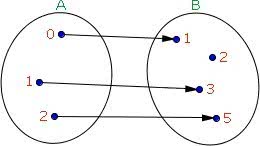
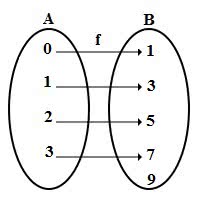
Funciones dadas: F de A = {0, 1, 2, 3} a B = {1, 3, 5, 7, 9} definida por la ley f (x) = 2x + 1. En el diagrama tenemos:
Tenga en cuenta que todos los elementos de la función A tienen contrapartes en B, sin embargo, uno de ellos no tiene comparación (9).
Gráfico
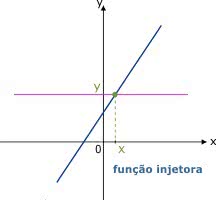
En la función de inyector, el gráfico puede aumentar o disminuir. Está determinada por una línea horizontal que pasa por un solo punto. Esto se debe a que un elemento de la primera función tiene un elemento correspondiente en la otra.
Lea también sobre ¿qué es la función?
Ejercicios de examen de ingreso con comentarios
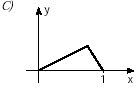
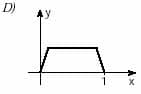
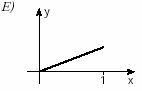
1. (Unifesp) Hay funciones y = f (x) que tienen la siguiente propiedad: “a valores distintos de X corresponden distintos valores de y”. Estas funciones se denominan inyectores. ¿Cuál de las funciones cuyas gráficas aparecen a continuación está inyectando?
dos. (IME-RJ) Considere los conjuntos A = {(1,2), (1,3), (2,3)} y B = {1, 2, 3, 4, 5}, y sea la función f: A → B tal que f (x, y) = x + y.
Es posible decir que f es una función:
a) inyector.
b) sobreyectiva.
c) biyector.
d) par.
e) extraño.
3. (UFPE) Sea A un conjunto con 3 elementos y B un conjunto con 5 elementos. ¿Cuántas funciones de inyector de A a B hay?
Descubra otros tipos de funciones: