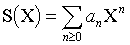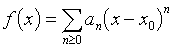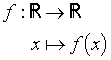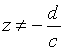función latina functio -onis de hongos cumplir

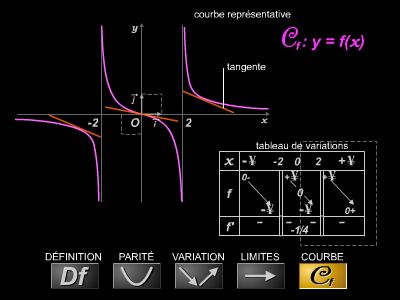
La noción de «función» se aplicó primero sólo a las funciones reales de la variable real. Las notaciones son entonces

.

Distinguimos el funciones racionales como funciones afines, funciones polinómicas, etc. ; sus imágenes solo se definen utilizando las cuatro operaciones (+, –, × y :); los funciones irracionales donde, para las imágenes, aparecen números irracionales. Estas dos categorías son funciones algebraicas. Las siguientes son funciones trascendentes: funciones exponenciales; los funciones circulares; los funciones hiperbólicas.

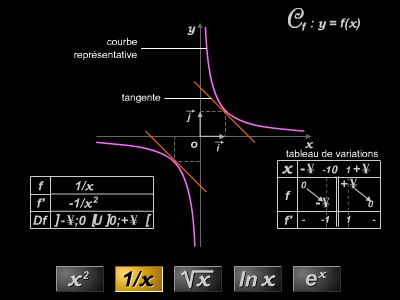
El estudio de una función numérica consiste en determinar su dominio de definición, los límites de la función en los límites de los intervalos que forman este dominio, los intervalos donde la función es creciente o decreciente. Estos resultados se registran en una tabla; en general, se realiza una representación gráfica de la función estudiada.

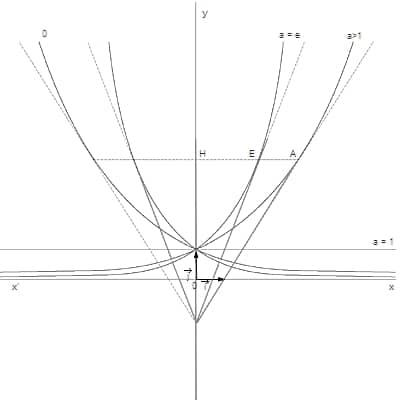
Función exponencial base a

Función que, cuando se define en ℝ, se obtiene como el recíproco de la función de logaritmo base Para. (Clasificación: Exp_Para.)

los funciones exponenciales básico Para definidas en ℝ deben sus propiedades a las de las funciones de logaritmo base Para. Así que si Para > 1, Iniciar sesión_Paraes una biyección continua y creciente de ℝ^{+ *}en ℝ: su función recíproca Exp_Paraes por tanto una biyección continua y creciente de ℝ en ℝ^{+ *}. Del mismo modo si 0 < Para <1, Iniciar sesión_Paraes una biyección continua y decreciente de ℝ a ℝ^{+ *} ; su función recíproca, Exp_Paraes por tanto una biyección continua y decreciente de ℝ en ℝ^{+ *}. Estas funciones son isomorfismos de (ℝ, +) en el grupo multiplicativo (ℝ^{+ *}, ×) : en particular

∀ (X, y) ∈ ℝ², Exp_Para (X + y) = exp_ParaX. Exp_Paray ;

Exp_Para 0 = 1 ; Exp_Para 1 = Para ;

∀X ∈ ℝ, exp_Para(-X) = 1 / exp_ParaX

y por lo tanto,

∀ (r, X) ∈ ℚ × ℝ, exp_Pararx = (exp_ParaX)^r.

Con respecto a lo que sucede en ℚ, nos vemos llevados a preguntar ∀ X ∈ ℝ, ∀ Para ∈ ℝ^{+ *}, Exp_ParaX = Para^X.

También obtenemos:

Exp_ParaX = Para^X = mi^{X. en Para},

∀ (X, y) ∈ ℝ², ∀ Para ∈ ℝ^{+ *} ;

Para^X. Para^y = Para^{X + y}y (Para^X)^y = Para^{X. y}.

La derivada de Exp_Paraentonces es la función

X ↦ Para^{X.ln Para}.

La función exponencial (exp) es la aplicación X ↦ mi^X, y su función derivada de la aplicación X ↦ mi^X ; por tanto, son iguales.

Función homografica

Función definida de ℂ en
mediante :

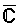
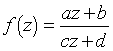
si z ≠ ∞ y

y
. (Especificamos función homográfica adecuada cuando anuncio – antes de Cristo ≠ 0, F siendo entonces biyectivo, o función homográfica inadecuada cuando anuncio – antes de Cristo = 0, F siendo entonces una función constante.)

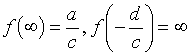
sí vs = 0, F es una semejanza o una traducción; si vs ≠ 0, la función homográfica propiamente dicha se compone de un número finito de mapas tomados de los siguientes tipos: traducción (z ↦ z + h), similitud (z ↦ k. z), inversión-simetría (z ↦ z⁻¹). Los mapeos homogéneos mantienen la relación cruzada.

Función positivamente homogénea de grado no

Función numérica definida en la parte D de un espacio vectorial E, verificando:

1 ° ∀ α ∈ ℝ⁺, si X ∈ D, entonces α. X ∈ D ;

2 ° ∀ α ∈ ℝ⁺, ∀ X ∈ D, F(α. X) = α^no. F(X). (También decimos más simplemente que F es homogéneo.)

El grado de homogeneidad de una función es un número racional. sí F es homogéneo de grado no en el espacio vectorial ℝ^pag, cada una de sus derivadas parciales, si existe, es homogénea de grado no – 1. El teorema de Euler da una propiedad de funciones homogéneas.

Función analítica de no variables

función F con valores reales o complejos, definidos en una D abierta y tales que F se puede desarrollar en serie completa en cualquier punto de D.

Propiedades de las funciones analíticas

Para una función analítica, existe en cualquier punto X₀ de D a real ρ (X₀)> 0 y una serie
, con un radio de convergencia mayor o igual a ρ (X₀), tal que
para | X – X₀ | <ρ (X₀). Una función analítica en D es indefinidamente diferenciable en D y sus derivadas sucesivas son analíticas en D.