Función logarítmica: todo lo que importa

1. definición
   

2. Matemáticas
3. ›
4. Roles

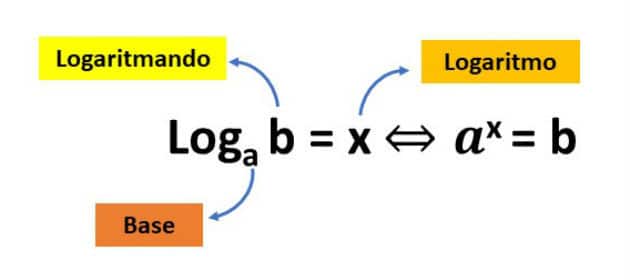
La función logarítmica base La se define como f (x) = log_La x, con La real, positivo y La ≠ 1. La función inversa de la función logarítmica es la función exponencial.

El logaritmo de un número se define como el exponente al que se debe elevar la base. La para obtener el número X, o sea:

Ejemplos de

• f (x) = registro₃ X
• g (x) =
• h (x) = registro₁₀ x = log x

Dominio de la función logarítmica

El dominio de una función representa los valores de x donde se define la función. En el caso de la función logarítmica, debemos tener en cuenta las condiciones de existencia del logaritmo.

Por lo tanto, el logaritmo debe ser positivo y la base también debe ser positiva y no igual a 1.

Ejemplo

Determine el dominio de la función f (x) = log_dos (x + 3).

Solución

Para encontrar el dominio, debemos considerar que (x + 3)> 0, debido a la condición de existencia del logaritmo. Resolviendo esta desigualdad, tenemos:

x + 3> 0 ⇒ x> – 3

Por tanto, el dominio de la función se puede representar mediante:

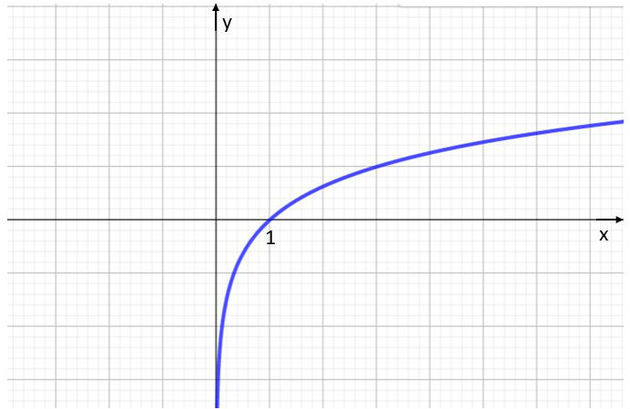
Gráfico de función logarítmica

En general, la gráfica de la función y = log_La x se ubica en los cuadrantes I y IV, ya que la función solo está definida para x> 0.

Además, la curva de la función logarítmica no toca el eje y y corta el eje x en el punto de abscisas igual a 1, ya que y = log_La1 = 0, para cualquier valor de La.

A continuación, presentamos un esquema de la gráfica de la función logarítmica.

Función ascendente y descendente

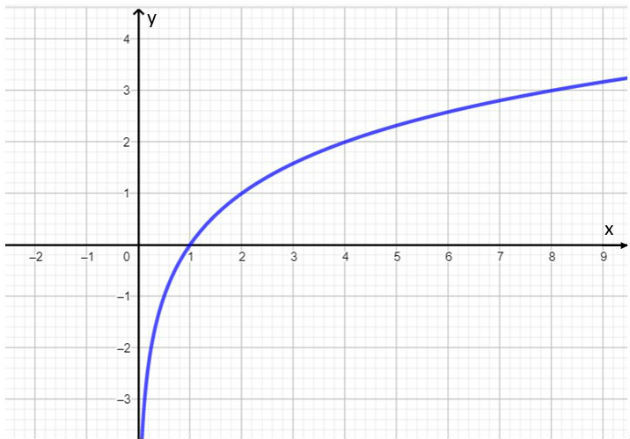
Una función logarítmica aumentará cuando la base La es mayor que 1, es decir, x₁ 2 ⇔ registro_La X₁hacha_dos. Por ejemplo, la función f (x) = log_dos x es una función creciente ya que la base es igual a 2.

Para verificar que esta función está aumentando, asignamos valores ax en la función y calculamos su imagen. Los valores encontrados se encuentran en la siguiente tabla.

Mirando la tabla, notamos que cuando el valor de x aumenta, su imagen también aumenta. A continuación, representamos el gráfico de esta función.

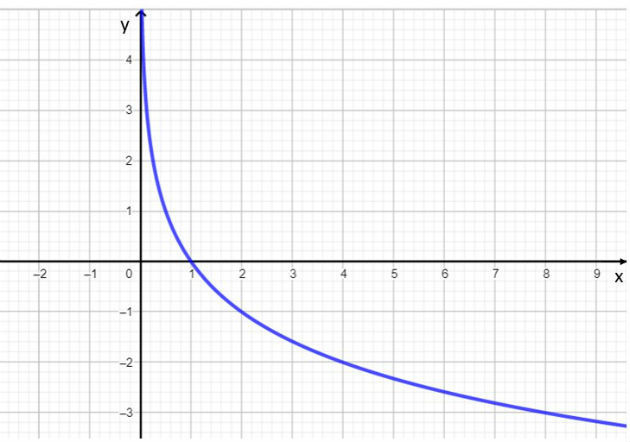
A su vez, las funciones cuyas bases son valores mayores que cero y menores que 1 son decrecientes, es decir, x₁ 2 ⇔ registro_La X₁ > registro_La X_dos. Por ejemplo, es una función decreciente porque la base es igual a .

Calculamos la imagen de algunos valores x de esta función y el resultado se muestra en la siguiente tabla:

Observamos que, mientras los valores de x aumentan, los valores de las respectivas imágenes disminuyen. De esta forma, encontramos que la función es una función decreciente.

Con los valores que se encuentran en la tabla, graficamos esta función. Tenga en cuenta que cuanto menor es el valor de x, más cercana a cero es la curva logarítmica, sin embargo, sin cortar el eje y.

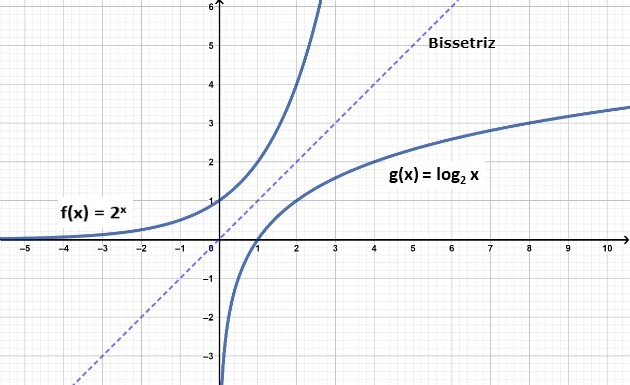
Funcion exponencial

La inversa de la función logarítmica es la función exponencial. La función exponencial se define como f (x) = a^X, con La positivo real y diferente de 1.

Una relación importante es que la gráfica de dos funciones inversas es simétrica en relación con la bisectriz de los cuadrantes I y III.

De esta forma, conociendo la gráfica de la función logarítmica con la misma base, por simetría podemos construir la gráfica de la función exponencial.

En el gráfico anterior, observamos que mientras la función logarítmica crece lentamente, la función exponencial crece rápidamente.

Ejercicios resueltos

1) PUC / SP – 2018

Las funciones , con k un número real, se intersecan en el punto . El valor de g (f (11)) es

2) Enem – 2011

La escala de magnitud de momento (abreviada como MMS y denotada como M_w), introducido en 1979 por Thomas Haks y Hiroo Kanamori, reemplazó a la Escala de Richter para medir la magnitud de los terremotos en términos de energía liberada. Menos conocido por el público, el MMS es, sin embargo, la escala utilizada para estimar las magnitudes de todos los grandes terremotos de hoy. Como la escala de Richter, el MMS es una escala logarítmica. METRO_w en_O relacionar por la fórmula:

donde M_O es el momento sísmico (generalmente estimado a partir de los registros de movimiento de superficie, a través de sismogramas), cuya unidad es la dina · cm.

El terremoto de Kobe, ocurrido el 17 de enero de 1995, fue uno de los terremotos que más impacto tuvo en Japón y en la comunidad científica internacional. Tenía magnitud M_w = 7.3.

Demostrando que es posible determinar la medida a través del conocimiento matemático, cuál fue el momento sísmico M_O del terremoto de Kobe (en dina.cm)

a) 10^{– 5.10}
b) 10^{– 0,73}
c) 10^12.00
d) 10^21,65
e) 10^27.00

Para obtener más información, consulte también: