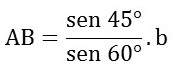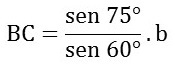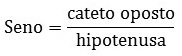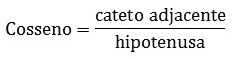Tabla de contenidos
La Ley de Senos determina que en cualquier triángulo, la razón sinusoidal de un ángulo es siempre proporcional a la medida del lado opuesto a ese ángulo.
Este teorema muestra que en el mismo triángulo la razón entre el valor de un lado y el seno de su ángulo opuesto siempre será constante.
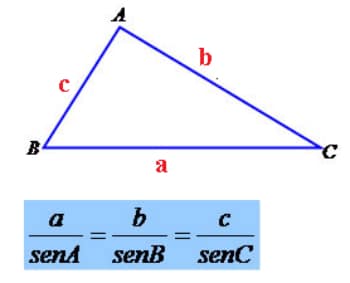
Así, para un triángulo ABC de lados a, b, c, la Ley de Senos admite las siguientes relaciones:
Ejemplo
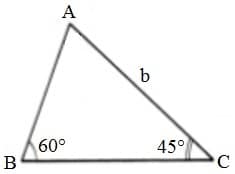
Para entender mejor, vamos a calcular la medida de los lados AB y BC de este triángulo, en función de la medida b del lado AC.
Por la ley de los senos, podemos establecer la siguiente relación:
Por lo tanto, AB = 0.816by BC = 1.115b.
Nota: Los valores del seno se consultaron en la tabla de razones trigonométricas. En él podemos encontrar los valores de los ángulos del 1º al 90º de cada función trigonométrica (seno, coseno y tangente).
Los ángulos de 30º, 45º y 60º son los más utilizados en los cálculos de trigonometría. Por tanto, se denominan ángulos notables. Consulte a continuación una tabla con los valores:
| Relaciones trigonométricas | 30 ° | 45 ° | 60 ° |
|---|---|---|---|
| Seno | 1/2 | √2 / 2 | √3 / 2 |
| Coseno | √3 / 2 | √2 / 2 | 1/2 |
| Tangente | √3 / 3 | 1 | √3 |
Aplicación de la Ley de senos
Usamos la Ley de Senos en los triángulos agudos, donde los ángulos internos son menores de 90º (agudos); o en triángulos obtusangulares, que tienen ángulos internos mayores a 90º (obtusos). En tales casos, también es posible utilizar la Ley del coseno.
El propósito principal de usar la Ley de Senos o Cosenos es descubrir las medidas de los lados de un triángulo y también, de sus ángulos.
Representación de triángulos según sus ángulos internos
¿Y la Ley de Senos en el Triángulo Recto?
Como se mencionó anteriormente, la Ley de los senos se usa en ángulos agudos y obtusos.
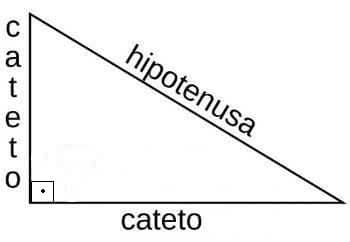
En los triángulos rectángulos, formados por un ángulo interno de 90º (derecha), utilizamos el Teorema de Pitágoras y las relaciones entre sus lados: opuesto, adyacente e hipotenusa.
Representación del triángulo rectángulo y sus lados.
Este teorema tiene la siguiente declaración: «la suma de los cuadrados de sus piernas corresponde al cuadrado de su hipotenusa«. Su fórmula se expresa:
Hdos = cados + codos
Así, cuando tenemos un triángulo rectángulo, el seno será la razón entre la longitud del lado opuesto y la longitud de la hipotenusa:
El lado opuesto se lee sobre la hipotenusa.
El coseno, por otro lado, corresponde a la proporción entre la longitud del cateto adyacente y la longitud de la hipotenusa, representada por la expresión:
Se lee el tramo adyacente a la hipotenusa.
Ejercicios
1. Calcula el seno del ángulo más grande de un triángulo cuyos lados miden 4.6 y 8 metros.
a) √15 / 4
b) 1/4
c) 1/2
d) √10 / 4
e) √3 / 2
dos.Una parcela de forma triangular tiene un frente de 10 my 20 m, en calles que forman un ángulo de 120º entre ellas. La medida del tercer lado del terreno, en metros, es:
a) 10√5
b) 10√6
c) 10√7
d) 26
e) 20√2
3. El lado más corto de un paralelogramo, cuyas diagonales miden 8√2 my 10 my forman un ángulo de 45º entre ellas, mide:
a) √13 m
b) √17 m
c) 13√2 / 4 m
d) 17√2 / 5 m