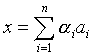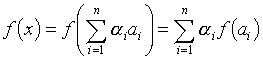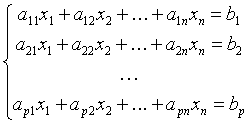lineal latín linearis de linea línea

MATEMÁTICAS

aplicación lineal

Si E y F son dos espacios vectoriales sobre un campo conmutativo K, y F un mapa lineal de E a F, por la primera propiedad F(X + allí) = F(X) + F(allí), F es un homomorfismo de grupo de (E, +) dentro (F, +) y por lo tanto tiene las mismas propiedades que los homomorfismos, en particular

F(0_mi) = 0_F, F(-X) = −f(X).

Por aplicación lineal F, la imagen de un subespacio vectorial de E es un subespacio vectorial de F. Un caso especial es la imagen F(MI) de E, señaló Estoy(F). La propiedad » F es sobreyectiva” es entonces equivalente a Estoy(F) = F.

Por aplicación lineal F, la imagen inversa de un subespacio vectorial de F es un subespacio vectorial de E. Un caso particular es la imagen inversa del subespacio formado por el elemento neutro 0_Fde F, generalmente llamado el núcleo de F y señaló Ker(F). La propiedad » F es inyectiva” es equivalente a Ker(F) = 0_mi.

sí
y
son respectivamente bases de E y F, F está enteramente determinada por el conocimiento de las coordenadas en (B_I) de cada uno de no vectores F(en_I). De hecho, si X es un elemento de E, tenemos

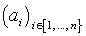
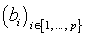
y

∀I ∈ { 1, …, no}, F(en) elemento de F se expresa como una combinación lineal de los vectores base (B_I). Llamamos matriz de la aplicación lineal F en comparación con las matrices (en_I) y (B_I) la matriz tipo (p-n) cuya columna de índice I está formado por las coordenadas de F(en_I) sobre la base (B_I).

Ecuación lineal

sí F es un mapa lineal de un espacio vectorial K E a un espacio vectorial K F y B un elemento de F, la ecuación F(X) = B tiene soluciones si F⁻¹ (B);≠ . La ecuacion F(X) = 0, llamada ecuación lineal homogénea asociada con F, admite por solución los elementos de Ker F. sí X₀es una solución de la ecuación F(X) = B, se tiene F(X − X₀) = 0_F, y X = X₀ ∈ Ker F ; Si X₀es una solución de F(X) = B, las otras soluciones son por lo tanto de la forma X₀ + z, o z ∈ Ker F.

Sistema de ecuaciones lineales

un sistema de pags ecuaciones lineales a no las incógnitas se pueden poner en la forma

.

La matriz EN [a_ij] es dicho matriz de coeficientes. Si denotamos por B la matriz columna de elementos B₁, B₂, …, B_pags y por X la matriz columna de elementos X₁, X₂, …, X_no, el sistema es equivalente a la igualdad matricial AX=B.

Un sistema lineal de no ecuaciones a no incógnitas cuya matriz A tiene un determinante distinto de cero, admite una única solución dada por la relación matricial X = A⁻¹. B o EN⁻¹es la matriz inversa de A.