Tabla de contenidos
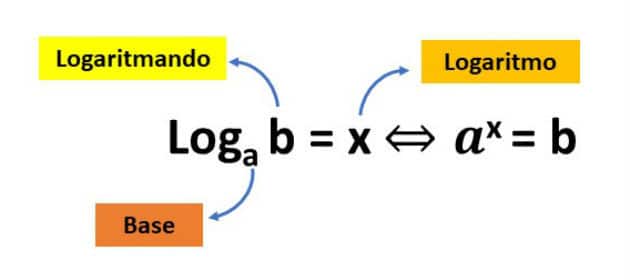
Logaritmo de un número b en base a es igual al exponente x al que debe elevarse la base, de modo que la potencia aX igual ab, siendo ayb números reales y positivos y a ≠ 1.
De esta forma, el logaritmo es una operación en la que queremos descubrir el exponente que debe tener una base dada para dar como resultado una determinada potencia.
Por ello, para realizar operaciones con logaritmos es necesario conocer las propiedades de la potenciación.
Definición de logaritmo
El logaritmo de b se lee en base a, con a> 0 y a ≠ 1 y b> 0.
Cuando se omite la base de un logaritmo, significa que su valor es igual a 10. Este tipo de logaritmo se llama logaritmo decimal.
¿Cómo calcular un logaritmo?
El logaritmo es un número y representa un exponente dado. Podemos calcular un logaritmo aplicando directamente su definición.
Ejemplo
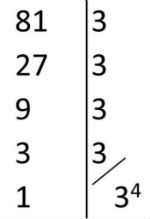
¿Cuál es el valor del registro?3 81?
Solución
En este ejemplo, queremos averiguar qué exponente debemos elevar a 3 para que el resultado sea igual a 81. Usando la definición, tenemos:
Iniciar sesión3 81 = x ⇔ 3X = 81
Para encontrar este valor, podemos factorizar el número 81, como se indica a continuación:
Reemplazando 81 con su forma factorizada, en la ecuación anterior, tenemos:
3X = 34
Dado que las bases son las mismas, concluimos que x = 4.
Consecuencia de la definición de logaritmos
- El logaritmo de cualquier base, cuyo logaritmo sea igual a 1, el resultado será igual a 0, es decir, logLa 1 = 0. Por ejemplo, log9 1 = 0, porque 90 = 1.
- Cuando el logaritmo es igual a la base, el logaritmo será igual a 1, por lo tanto, logLa a = 1. Por ejemplo, log5 5 = 1, porque 51= 5
- Cuando el logaritmo de La en la base La tiene una potencia m, será igual al exponente m, es decir, logLa Lametro = m, porque usando la definición ametro = ametro. Por ejemplo, log3 35 = 5.
- Cuando dos logaritmos con la misma base son iguales, los logaritmos también serán iguales, es decir, logLa b = registroLa c ⇔ b = c.
- La potencia base ay el exponente logarítmicoLa b será igual ab, es decirIniciar sesiónLaB = b.
Propiedades de los logaritmos
- Logaritmo de un producto: El logaritmo de un producto es igual a la suma de sus logaritmos: LogLa (bc) = RegistroLa b + logLa C
-
Logaritmo de un cociente: El logaritmo de un cociente es igual a la diferencia de los logaritmos: LogLa
= RegistroLa BlogLa C
- Logaritmo de una potencia: El logaritmo de una potencia es igual al producto de esa potencia por el logaritmo: LogLa Bmetro = m. TroncoLa B
-
Cambio de base: Podemos cambiar la base de un logaritmo usando la siguiente relación:
EJEMPLOS
1) Escribe los siguientes logaritmos como un solo logaritmo.
un registro3 8 + registro3 10
Blogdos 30 – registrodos 6
c) 4 log4 3
Solución
un registro3 8 + registro3 10 = registro3 8.10 = registro3 80
B)
c) 4 log4 3 = registro4 34 = registro4 81
2) Escribe el registro8 6 usando el logaritmo en base 2
Solución
Cologaritmo
La llamada cologaritmo es un tipo especial de logaritmo expresado por la expresión:
coloniaLa b = – registroLa B
También podemos escribir eso:
Para obtener más información, consulte también:
Curiosidades sobre los logaritmos
- El término logaritmo proviene del griego, donde “logos«Significa razón y»aritmos”Corresponde al número.
- Los creadores de los logaritmos fueron John Napier (1550-1617), matemático escocés, y Henry Briggs (1531-1630), matemático inglés. Crearon este método para facilitar los cálculos más complejos que se conocieron como «logaritmos naturales» o «logaritmos neperianos», en referencia a uno de sus creadores: John Napier.
Ejercicios resueltos
1) Sabiendo que el , calcula el valor del registro9 64.
2) UFRGS – 2014
Asignando log 2 a 0.3, los valores log 0.2 y log 20 son, respectivamente,
a) – 0,7 y 3.
b) – 0,7 y 1,3.
c) 0.3 y 1.3.
d) 0,7 y 2,3.
e) 0,7 y 3.
Para obtener más preguntas sobre logaritmos, consulte Logaritmo: ejercicios.