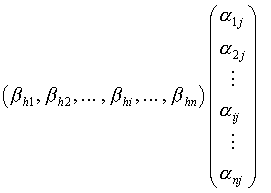Tabla de contenidos
(Latín matriz, aquí)
Familia (αij) elementos de un campo K, (I, j) ∈ {1,…, no } × {1,…, pag}, no y pag siendo dos naturales, generalmente presentados en forma de una matriz rectangular con no líneas y pag columnas [matrice de type (n, p)].
MATEMÁTICAS
sí M = (αij) es una matriz de tipo (no, pag), el elemento αijestá en la intersección de la Ith línea y jth columna. Los elementos de la misma fila forman un vector de fila; los elementos de la misma columna forman un vector de columna.
sí no = 1, la matriz se llama matriz de filas;
si pag = 1, la matriz se llama matriz de columnas;
si no = pag, la matriz se llama matriz cuadrada de orden no.
Los elementos αiide una matriz cuadrada, llamados elementos diagonales, forman la diagonal principal de la matriz. Si los elementos ubicados simétricamente con respecto a esta diagonal son iguales (αij = αJi), se dice que la matriz es simétrica.
El conjunto de matrices de tipos (no, pag) en un campo se anota K METROn, p(K). El conjunto de matrices cuadradas de orden no en un campo se anota K METROno(K).
Estructura del conjunto Mn, p(K)
La suma de dos matrices M = (αij) y M ′ = (α ′ij) es definido por M + M ′ = (βij) con βij = αij + α ′ij. La multiplicación externa de una matriz M = (αij) por un escalar λ se define por λM = (βij), con βij = λαij. Equipado con estas dos operaciones, el conjunto METROn, p(K) tiene una estructura de espacio vectorial en K de dimensión notario público. El elemento neutro del grupo aditivo es la matriz nula, generalmente anotada como 0, que satisface ∀ (I, j), αij = 0, y el opuesto de la matriz M = (αij) es la matriz, denotada −M, igual a (−αij). sí M = (αij) es un elemento de METROn, p(K) y N = (βHola) un elemento de METROm, n(K), entonces el producto NM se define por NM = (γhj), o
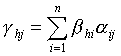
; entonces tenemos:
γhj = βh1 α1j + βh2 α2j +… + ΒHola αij +… + Βhn αNueva Jersey.
Evidentemente, esta multiplicación entre matrices no es conmutativa.
Estructura del conjunto Mno(K)
El producto de dos matrices cuadradas de orden no siempre está definido; todos METROno(K) matrices cuadradas de orden no, provisto de las operaciones de suma y multiplicación de las matrices, es por tanto un anillo unitario. El elemento unitario es la matriz unitaria, anotado Ino, cuyos elementos diagonales son iguales a 1, siendo todos los demás elementos cero. Este anillo no es conmutativo y no es integral. Equipado con las tres operaciones suma, multiplicación y multiplicación externa por un escalar λ, tiene una estructura algebraica en K. Sus elementos invertibles son las matrices asociadas con automorfismos; se denominan matrices cuadradas regulares o invertibles.
Las matrices juegan un papel importante en el álgebra lineal (estudio de mapas lineales, endomorfismos, automorfismos, determinantes) y en la resolución de sistemas de ecuaciones lineales. También encuentran muchas aplicaciones en física y análisis numérico (análisis teórico de la estabilidad de métodos de cálculo numérico, resolución numérica de sistemas de ecuaciones lineales, ecuaciones diferenciales y diferenciales parciales, etc.).