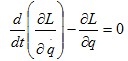Mecánica clásica – Física –

La física intenta explicar los fenómenos naturales a partir del análisis de cada sistema aislado. Cada uno de estos sistemas obedece a un cierto conjunto de leyes que gobiernan los fenómenos que cambian la configuración de los componentes del sistema a lo largo del tiempo. En algunos casos, es más conveniente utilizar la mecánica newtoniana, utilizando un sistema de coordenadas cartesiano. Pero, en general, los fenómenos requieren herramientas poderosas que pueden tener una aplicación más general. Para ello es necesario escribir las ecuaciones de movimiento de cualquier sistema utilizando coordenadas generalizadas.

Cada partícula tiene tres coordenadas, en el sistema cartesiano. Pero para n partículas, un espacio llamado espacio de configuración, que tiene coordenadas 3n. Así, en lugar de n cuerpos con tres coordenadas, el sistema se ocupará de un cuerpo con 3n coordenadas generalizadas. Por ejemplo, un problema de 2 cuerpos y tres ejes de coordenadas se puede describir como el problema de un cuerpo con seis coordenadas generalizadas, dadas por 3n, de modo que 3n = 3.2 = 6, donde n es el número de cuerpos y el factor 3 corresponde a las tres coordenadas del sistema cartesiano. (LEECH, JW, según OLIVEIRA, 1971.)

Pero aparentemente sería más difícil resolver un problema con seis coordenadas. Pero hay artificios para eliminar algunos de ellos, ya que no serán necesarios para solucionar el problema. Esto se debe a que existen algunas restricciones a la libre circulación del sistema, llamadas enlaces.

Entre las formulaciones más utilizadas por la Mecánica clásica, destacan las formulaciones de Lagrange, Hamilton y Jacobi. Estos fueron los encargados de crear nuevas herramientas para aplicar en los estudios de fenómenos físicos en sistemas complejos. Estas herramientas sirven para eliminar las dificultades en el cálculo de vectores de sistemas en movimiento. Pero, ¿cómo podría ser esto posible? Bueno, en primer lugar es necesario realizar una transformación de coordenadas, transcribiendo el sistema utilizando coordenadas con todas las variables en forma escalar. Para ello, el sistema se escribe en función de la energía. También es interesante eliminar las variables no deseadas escribiendo ecuaciones de enlace, que eliminan las llamadas fuerzas de enlace.

Al eliminar los enlaces, se reduce el número de grados de libertad en el sistema. Tendremos S ecuaciones de movimiento para cualquier sistema, de modo que S = 3.n – P, donde n es el número de cuerpos que componen el sistema y P es el número de enlaces.

Un ejemplo de una ecuación de enlace muy conocida es la ecuación del círculo, que limita el movimiento de un objeto a una distancia constante desde un punto fijo, dada por el radio de la circunferencia en cuestión. En el caso de la Máquina Atwood, sería la longitud de un conector inextensible que conecta las dos masas. Para estas ecuaciones, ya se puede eliminar una variable en uno de los ejes de coordenadas, ya que el movimiento se puede restringir a un plano. Considerando el plano xy, tendríamos para el objeto que se mueve en el círculo:

x² + y² = R

z = 0

Esto implica solo una ecuación de Lagrange para este problema, porque al establecer S = 3.n – P, tenemos S = 3.1 – 2, ya que tenemos dos ecuaciones vinculantes.

Y para la máquina Atwood, tendríamos las siguientes restricciones a la libre circulación del sistema:

z = 0

y₁ + y_dos = 1

Es decir, la longitud del cable viene dada por la suma de las distancias desde cada masa hasta el punto de apoyo. En este caso, también tendremos una sola ecuación de Lagrange. Tenga en cuenta que en estos dos problemas tenemos vínculos holonómicos y escleronómicos, ya que pueden escribirse por igual y son independientes del tiempo.

Cuando es conveniente, transforma las coordenadas de un sistema de coordenadas cartesiano a cilíndrico o esférico. Generalmente, se utilizan ecuaciones de transformación conocidas. Ejemplo: para el círculo, tendremos un ángulo θ y un radio R. Como el sistema está restringido a un plano, podemos escribir en coordenadas cilíndricas. Así tendremos:

x = R.cosθ

y = R.senθ

z = 0

En la formulación lagrangiana se utilizan básicamente la energía cinética T y la energía potencial V implicadas. La diferencia entre la energía cinética es la ecuación de Lagrange como se muestra en la siguiente ecuación.

L = T – V

Para resolver esta ecuación, se debe cumplir la siguiente propiedad:

En el caso de la formulación hamiltoniana, utiliza la energía total del sistema, dada por la siguiente ecuación.

H = T + V

Esto es válido para sistemas conservadores con el sistema de coordenadas independiente del tiempo, es decir, fijo en el espacio.

Para llegar a las ecuaciones de movimiento por la formulación de Hamilton, satisfaga las propiedades escritas a continuación, donde posiblemente aparecerán coordenadas innobles o cíclicas.

(Forma canónica de Hamilton de las ecuaciones de movimiento)

Referencias bibliográficas:
LEECH, JW, BSc. Doctor. Mecánica analítica. Traducción de OLIVEIRA, Carlos Campos de. Ed. Al libro técnico SA y Editora da Universidade de São Paulo. Río de Janeiro, 1971. 160p.