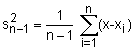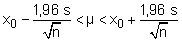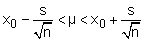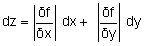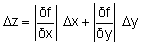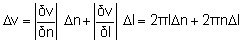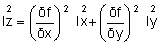Tabla de contenidos
(Latín medida)
Relación numérica de una cantidad a otra cantidad de la misma naturaleza tomada como unidad; ubicar la posición de una cantidad conocida como localizable en una escala aceptada por convención, incluso si uno no sabe cómo definir la relación con una unidad.
METROLOGÍA
Una medida se realiza con un instrumento de comparación y una serie de objetos calibrados, haciendo una serie de relaciones por unidad conocidas (escala y masas marcadas, cajas de resistencias, etc.), o con un instrumento de escala graduada y calibrada (calibre, automático). balanza, voltímetro, etc.). Dado que las causas de error son múltiples, se utilizan métodos adecuados (doble pesaje) para reducir su importancia y se aplican correcciones compensatorias (corrección de calibración, corrección de temperatura, etc.). Los errores residuales y aleatorios se estudian utilizando un enfoque estadístico; se caracterizan por un margen de incertidumbre. (→ metrología.)
Incertidumbre de las medidas
En una serie de medidas, la dispersión, es decir, las diferencias observadas de una medida a otra, tiene causas diversas. Los errores de las medidas físicas se deben principalmente a: 1. los errores del observador: mala lectura, etc.; ; 2. errores personales, por ejemplo, demora en poner en marcha un cronómetro; 3. a errores estocásticos, siempre presentes, que provienen de la limitación de instrumentos, movimiento browniano, interferencia de fuentes o medios externos, efectos cuánticos, etc. ; 4. errores sistemáticos, que surgen de errores de calibración o efectos despreciados. Los errores sistemáticos son los más graves y, a menudo, los más difíciles de detectar. Los métodos de la estadística se aplican a los errores, en particular para determinar el error estándar del resultado de un experimento.
Errores sistemáticos
Algunos provocan una desviación siempre orientada en la misma dirección (positiva o negativa) con respecto al valor de referencia: este es el caso de una calibración incorrecta o ajustes a cero del dispositivo de medición. Así, si utilizamos una báscula que indique 1 kg vacío, el peso será incorrecto en cada pesaje, y siempre sobrestimado. Estos errores dicen sistemático, generalmente se puede corregir (mediante un ajuste a cero, por ejemplo).
Errores aleatorios
Después de la corrección, puede quedar una dispersión: al pesarse varias veces seguidas, a veces observamos algunas variaciones, porque se han producido pequeñas desviaciones en una dirección u otra sin poder saber las causas. Estas pequeñas desviaciones producen dispersión. Se designan por la expresión deerrores aleatorios, expresión que indica que cierta parte del azar está ligada al fenómeno de la dispersión.
Teniendo en cuenta los errores en la medición
La distinción entre error sistemático y error aleatorio suele ser difícil de establecer, hasta el punto de que un procedimiento común consiste en cometer errores aleatorios que generalmente se clasifican como sistemáticos, pero que no se pueden corregir. Esto implica el uso de una gran cantidad de dispositivos de medición para que las variaciones registradas ya no puedan atribuirse a fallas en un solo dispositivo sino a las diferencias aleatorias que existen de un dispositivo a otro.
Para entender por qué los físicos utilizan la noción de azar en la descripción de este fenómeno, tenemos que imaginar qué pasaría si hiciéramos un número infinito de medidas. Esto corresponde en estadística a una población de la que se extrae una muestra de n mediciones. Los valores que componen los llamados parentesco se agrupan alrededor de un valor central, con algunos valores que se desvían de él. Esto aparece si representamos los resultados mediante un histograma, ya sea una infinidad de pesajes de una misma persona, medidas de una intensidad con una infinidad de amperímetros, o cualquier otra serie de medidas. La cifra obtenida se aproxima a un histograma simétrico: corresponde a la distribución estadística gaussiana que ilustra la teorema del límite central, Donde del límite centrado, que se verifica sujeta a ciertas condiciones en cuanto a los métodos de ejecución de las medidas (en particular, deben ser independientes entre sí).
El objetivo de eliminar los errores sistemáticos de la forma más completa posible es mejorar la calidad del resultado y hacerlo lo más preciso posible. Tratar de deshacerse de los errores aleatorios equivale a mejorar otra cualidad del resultado de la medición, la precisión.
La oportunidad de las medidas
Hay fenómenos físicos para los que es difícil hacer predicciones, porque su naturaleza hace que la mínima variación de las condiciones iniciales modifique el resultado del experimento. Es el caso de un proyectil que parece lanzarse siempre de la misma manera y que nunca cae exactamente en el mismo lugar, o de una bola lanzada sobre un obstáculo cilíndrico (un clavo, por ejemplo).
El físico se enfrenta a fenómenos que, aunque obedecen a leyes deterministas, tienen resultados impredecibles: dice entonces que el resultado es aleatorio y que es el azar determinista el que gobierna estos fenómenos; las estadísticas permiten predicciones no de cada experimento sino, como un todo, de un conjunto de experimentos.
La herramienta estadística y la precisión
Los teoremas estadísticos muestran que varias medidas pueden mejorar la calidad de la información recopilada.
Estos teoremas explotan el resultado según el cual el histograma de la población de medidas corresponde a la representación gráfica de la ley de probabilidad de Gauss, que es una función matemática P (x), normalizada (es decir, cuya área entre la curva y el eje x es igual a 1), simétrica con respecto a un valor central μ, y definida por la cantidad σ (σ2 es la varianza de la distribución).
El punto de inflexión es el punto de la curva donde la curvatura cambia de dirección; matemáticamente, la segunda derivada se anula en este punto.
Las tablas dan el valor de estas funciones para cualquier valor de x. Otras tablas permiten calcular cualquier área entre la curva de Gauss, el eje x y el eje de las paralelas al eje y. Por lo tanto, los siguientes resultados numéricos se utilizan a menudo en la teoría de la medición en dos formas: el valor de las áreas y la interpretación en términos de probabilidades.
En realidad, nunca tomamos una infinidad de medidas, sino que estudiamos una muestra de n medidas. Probamos que el mejor representante de tal serie, lo que los estadísticos llaman el mejor estimador del valor central de la población, es su media, x0. Asimismo, el mejor estimador de la varianza de la población padre corresponde a un valor s, tal que (con n > 1):
la media x0 y la raíz de la desviación cuadrática media sno–1 (a menudo notado s) son dados por calculadoras equipadas con funciones estadísticas. Obtenidos estos dos valores, podemos calcular un intervalo en el que el centro μ de la población padre tiene un 95% de posibilidades de ser encontrado (o un 68% o cualquier otro porcentaje que den las tablas numéricas). Por ejemplo, para más de 20 mediciones, el valor μ tiene:
95% de probabilidad de verificar
68% de posibilidades de pasar
Los coeficientes 1,96 y 1 multiplicando s deben ser reemplazados por otros coeficientes si n es menor que un valor que tomamos aproximadamente igual a 20: por ejemplo, 1,96 debe ser reemplazado por 2,26 si no tenemos solo 10 medidas, y por 2,77 si solo hay 5 medidas.
Mejorar el resultado de una medición
La calidad de una medición depende de dos factores: la precisión, que depende de las técnicas de cálculo empleadas, y la exactitud, que está determinada por las condiciones en las que se realiza la medición. La herramienta estadística mejora la precisión. Las fórmulas muestran que esto depende de dos factores, la varianza de las n medidas tomadas y el número n de medidas: cuanto mayor es n, más se reducen los efectos de los errores aleatorios, más se mejora la precisión. Así, si pasamos de una serie de n medidas a una serie de 100 n medidas, la amplitud del intervalo de confianza correspondiente a la misma tasa de confianza se divide por 10. De hecho, es bastante inútil llevar demasiado lejos la búsqueda de la precisión si uno no tiene los medios para mejorar la precisión de la misma manera. Por lo tanto, sería absurdo pesarse 100 veces seguidas en una báscula de baño que no tenga una configuración de vacío confiable. La precisión se mejora al minimizar los errores sistemáticos, lo que requiere una reflexión sobre el fenómeno en sí y sobre el método de medición. Los histogramas asociados (figura siguiente) presentan una y/u otra cualidad. Multiplicar las medidas en el primer caso no aportaría ninguna información adicional, dada la imprecisión ligada a las condiciones de la medida.
Transmisión de incertidumbres
El siguiente problema surge con frecuencia durante las operaciones de medición: si una cantidad z es una función de otras cantidades, por ejemplo x e y, y si x e y están sujetas a incertidumbre, entonces se puede escribir en la forma z = f (x, y) también está teñido de incertidumbre. Es necesario saber deducir Δz de Δx y Δy. Así es como la velocidad de rotación de un motor síncrono es proporcional a la frecuencia n de la corriente alterna que lo alimenta (ω = 2π n). Si es la corriente de red, cuya frecuencia de 50 Hz está garantizada por EDF dentro de 1 Hz, la velocidad de rotación del motor estará garantizada en 2π rad/s, o 6,28 rad/s. Esta incertidumbre también se transmite a otras magnitudes, como la velocidad lineal del extremo de un brazo accionado por el eje del motor. En este ejemplo, la velocidad lineal del extremo de un brazo de 50 cm es constante con una precisión de 3,14 m/s.
El problema de la transmisión de incertidumbres se trata matemáticamente: en efecto, se considera que son pequeñas variaciones alrededor del valor de referencia, y se utiliza el cálculo diferencial. Entonces podemos escribir, por ejemplo para dos variables:
(las derivadas parciales se calculan para los valores medios de x e y medidos).
Esta fórmula muestra que cada una de las variables contribuye a la incertidumbre sobre z. Se desarrolla de manera diferente según el conocimiento de que se tienen incertidumbres sobre x y sobre y.
– En un primer caso, conocemos las incertidumbres Δx y Δy. Se tiene :
Δz aparece así como la suma de contribuciones incertidumbres sobre x y sobre y.
Puede aplicarse al caso del motor mencionado anteriormente, donde v es la velocidad lineal del brazo; v = 2π nl (siendo l la longitud del brazo). EDF garantiza Δn = 1 Hz, y la longitud del brazo se puede conocer con una precisión de 1 mm, por lo tanto, Δl = 0,001 m.
¿Cuál es Δv para el motor?
Con los valores numéricos dados anteriormente, obtenemos: Δv = (3,14 + 0,314) m/s. Nos damos cuenta de que la incertidumbre debida a la frecuencia es 10 veces mayor que la debida a la longitud: las contribuciones son muy diferentes.
– Otro caso es aquel donde se han realizado varias medidas de x e y. Luego calculamos el intervalo de confianza para x y para y (es decir, Ix e Iy), y podemos escribir una fórmula que proporcione una buena evaluación del intervalo de confianza para z (es decir, Iz) bajo algunas condiciones:
Como antes, cada una de las variables contribuye al intervalo de confianza de la función.
Por ejemplo, si 20 estudiantes buscan el valor de la misma resistencia R midiendo la corriente J y el voltaje V, cada uno a su vez puede decir:
J tiene un 95% de posibilidades de estar en el intervalo Ij ;
V tiene un 95% de posibilidades de estar en el intervalo IV ;
Por lo tanto, R tiene un 95% de posibilidades de estar en el intervalo (Ij2 + yoV2)1/2.
Se notará que estos cálculos son válidos en el caso en que las cantidades x e y sean independientes; de lo contrario, la transmisión de errores es más compleja.