Tabla de contenidos
(Latín número)

Noción que permite contar, enumerar cosas o seres, clasificar objetos, medir tamaños.
MATEMÁTICAS

Los números son uno de los inventos más asombrosos de la inteligencia humana desde muchos puntos de vista. Psicológico ante todo, el hecho de saber contar supone un proceso de abstracción que se forma lentamente. Entonces, la historia tomó muchas pruebas y mucho tiempo para que se implementara un sistema de numeración efectivo. Finalmente, filosóficamente, contar plantea el problema de la pluralidad y la identidad.
Los principios de la numeración.

La idea de contar por “paquetes” surgió bastante pronto; empezamos construyendo nuevos símbolos para cada uno de los “niveles”: 10, 100, 1000, etc. Este es el caso de la escritura egipcia, griega o romana. Este modo de representación conducía a un callejón sin salida: solo podías escribir un número grande si tenías el símbolo correspondiente. Además, no todos los sistemas formaban los «paquetes» de la misma manera: algunos cambiaban de «nivel», por ejemplo, al 10, otros al 12 o al 60. Encontramos un remanente de estas prácticas en las actuales medidas de tiempo y ángulo. El gran descubrimiento que dio origen al actual sistema de escritura de los números probablemente provenga de la India, transmitido y transformado por los árabes. Es una escritura posicional en la que los símbolos son pocos. El lugar de cada uno de ellos en el número indica su «nivel». Por lo tanto, gracias a este sistema, podemos escribir potencialmente cualquier número con la condición de tener (y crear) un signo para marcar la ausencia, el cero.
teoría de los números
Los números enteros forman la base sobre la que descansa el edificio matemático. Es por extensiones sucesivas de operaciones sobre números enteros que definimos todos los demás números. Sirven, a su vez, para definir la continuidad de los puntos de una recta y están en el origen de la teoría de funciones. Finalmente, estas funciones permiten, a través de la geometría analítica, traducir en ecuaciones cualquier problema sobre las figuras del espacio. Esto explica el lugar central que ocupa en matemáticas la aritmética, o teoría de los números. Desde un punto de vista lógico, la consistencia, es decir, la no contradicción de este último basta para garantizar la validez de todas las matemáticas.
Conjuntos de números
enteros
Forman una escala que comienza con un punto de partida, cero en los sistemas habituales, y continúa indefinidamente. Esta escala indica, por un lado, un orden: primero, segundo, tercero…, por otro lado, un tamaño: uno, dos, tres… A esta última función, llamada «cardinal», se vincula, el de operación (adición y multiplicación). La suma y el producto de dos números enteros siguen siendo números enteros. Podemos definir sus operaciones recíprocas (o inversas), la resta y la división. Sin embargo, en el conjunto ℕ de números enteros, estos últimos no siempre son posibles. Podemos calcular 7 − 5 pero no 5 − 7; de manera similar, podemos dividir 12 entre 4 pero no entre 5. Para superar esta dificultad, hemos extendido ℕ a numeros relativos entonces a numeros racionales, de tal manera que los cálculos sean siempre factibles.
Números relativos
Para dar sentido a una resta como 5 − 7, que es imposible para los números enteros, extendemos estos por una secuencia simétrica con respecto a 0; este se compone de los mismos números precedidos por un signo menos y se ingresan en orden inverso. Entonces el conjunto se escribe: {… − 4, − 3, − 2, − 1, 0, 1, 2, 3, 4…}. Este nuevo conjunto ℤ de números enteros se extiende indefinidamente en ambas direcciones; se compone de dos partes, la números negativos, precedido por un signo menos, y numeros positivos
Numeros racionales
Una división de A por B sólo es posible, con números enteros, si A es múltiplo de B. Cuando no es así, el método de extensión, que se usaba para las restas, lleva a preguntar este cociente como una nueva entidad definida precisamente por división: el cociente de 2 por 3, por ejemplo, es un racional en. Para que esta definición sea plenamente operativa, es necesario indicar cuáles son los criterios de igualdad entre estos nuevos números y cómo se pueden realizar operaciones con ellos. Su representación se realiza de dos formas: bien en forma de fracción (en se escribe entonces como 2/3), o en forma decimal (en es entonces igual a 0.666…).
Previamente hemos construido una secuencia de tres conjuntos, la de los números enteros ℕ, su extensión a los números relativos ℤ y, por último, la extensión de estos últimos a los números racionales ℚ. Con ℚ se realiza el cierre algebraico del conjunto de números enteros con respecto a las cuatro operaciones que naturalmente se definen en él. De hecho, el conjunto de los números racionales es el conjunto más pequeño que contiene los números enteros y en el que todas las operaciones definidas en ℕ así como sus inversas son posibles sin ninguna restricción.
numeros reales
Ya en la antigüedad griega se descubrió que ciertas cantidades resultantes de construcciones geométricas (por ejemplo
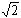
Números complejos
En el conjunto ℝ así constituido, queda sin embargo una operación imposible: el cálculo de la raíz cuadrada de un número negativo. Para superar esta imposibilidad, nos vemos obligados a construir los llamados números «imaginarios», como el número Iverificando por definición la relación: I2 = − 1. Por lo tanto, extendemos los números reales sumergiéndolos en un conjunto más grande en el que podemos extraer las raíces de cualquier número positivo o negativo. El conjunto obtenido es el conjunto ℂ de números complejos.