Tabla de contenidos
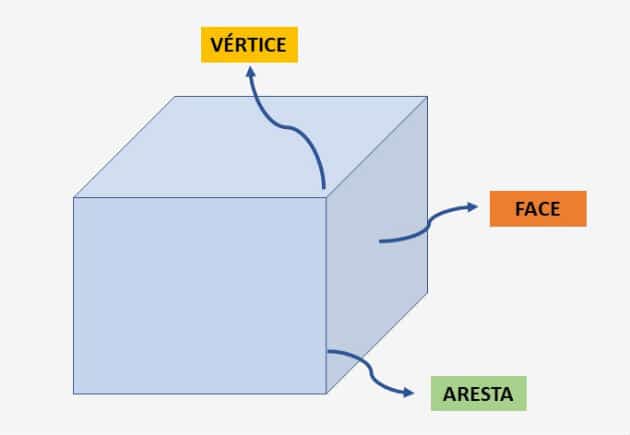
Los poliedros son sólidos geométricos limitados por un número finito de polígonos planos. Estos polígonos forman las caras del poliedro.
La intersección de dos caras se llama arista y el punto común de tres o más aristas se llama vértice, como se muestra en la imagen de abajo.
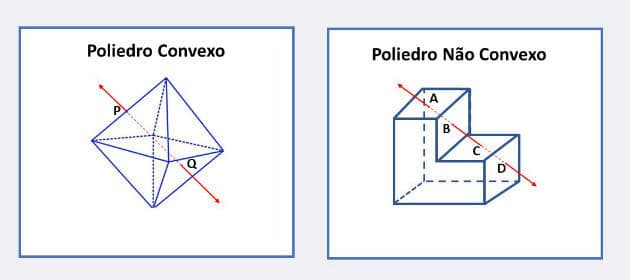
Poliedro convexo y no convexo
Los poliedros pueden ser convexos o no convexos. Si cualquier segmento de línea que conecta dos puntos de un poliedro está completamente contenido en él, entonces será convexo.
Otra forma de identificar un poliedro convexo es verificar que cualquier línea que no esté contenida o paralela a ninguna de las caras, corte los planos de las caras en un máximo de dos puntos.
Teorema de euler
O Teorema o relación de Euler es válido para poliedros convexos y para algunos poliedros no convexos. Este teorema establece la siguiente relación entre el número de caras, vértices y bordes:
F + V = 2 + A o V – A + F = 2
Dónde,
F: número de caras
V: número de vértices
LA: número de aristas
Los poliedros en los que es válida la relación de Euler se denominan eulerianos. Es importante tener en cuenta que todo poliedro convexo es euleriano, pero no todos los poliedros eulerianos son convexos.
Ejemplo
Un poliedro convexo está formado por exactamente 4 triángulos y 1 cuadrado. ¿Cuántos vértices tiene este poliedro?
Solución
Primero, necesitamos definir el número de caras y aristas. Como el poliedro tiene 4 triángulos y 1 cuadrado, tiene 5 caras.
Para encontrar el número de aristas podemos calcular el número total de lados y dividir el resultado entre dos, ya que cada arista es la intersección de dos lados:
Ahora que conocemos el número de caras y aristas, podemos aplicar la relación de Euler, así:
Por tanto, este poliedro tiene 5 vértices.
Poliedros regulares
Los poliedros convexos son regulares cuando sus caras están compuestas por polígonos regulares y congruentes. Además, el número de aristas que compiten en cada vértice es el mismo.
Debemos recordar que los polígonos regulares son aquellos que tienen todos los lados y ángulos congruentes, es decir, con la misma medida.
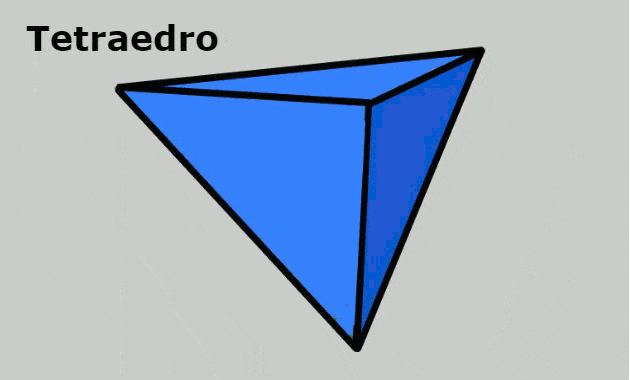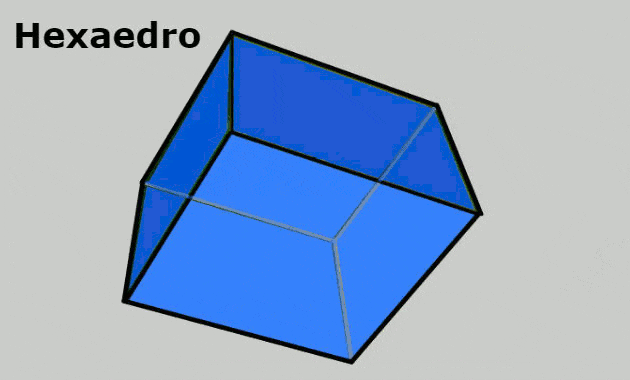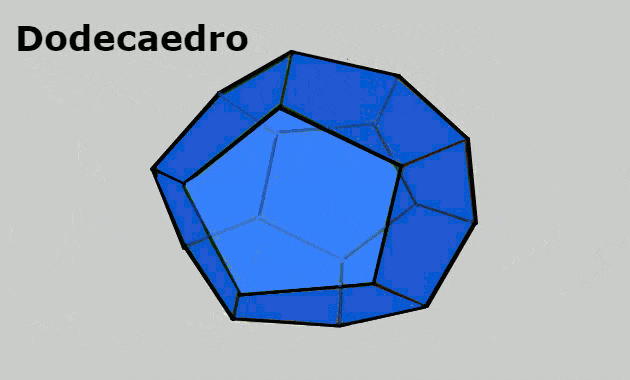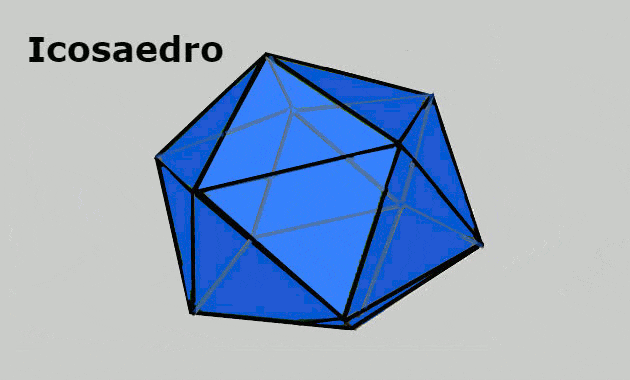
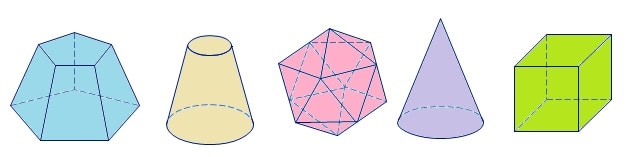
Solo hay cinco poliedros regulares convexos, que también se denominan «Sólidos platónicos«O»Poliedros de Platón”. Ellos son: tetraedro, hexaedro (cubo), octaedro, dodecaedro, icosaedro.
- Tetraedro: sólido geométrico formado por 4 vértices, 4 caras triangulares y 6 aristas.
- Hexaedro: sólido geométrico formado por 8 vértices, 6 caras cuadrangulares y 12 aristas.
- Octaedro: sólido geométrico formado por 6 vértices, 8 caras triangulares y 12 aristas.
- Dodecaedro: sólido geométrico formado por 20 vértices, 12 caras pentagonales y 30 aristas.
- Icosaedro: sólido geométrico formado por 12 vértices, 20 caras triangulares y 30 aristas.
Prismas
Los prismas son sólidos geométricos que tienen dos bases formadas por polígonos congruentes y ubicadas en planos paralelos. Sus caras laterales son paralelogramos o rectángulos.
Según la inclinación de los bordes laterales con respecto a la base, los prismas se clasifican en rectos u oblicuos.
Las caras laterales de los prismas rectos son rectángulos, mientras que los prismas oblicuos son paralelogramos, como se muestra en la siguiente imagen:
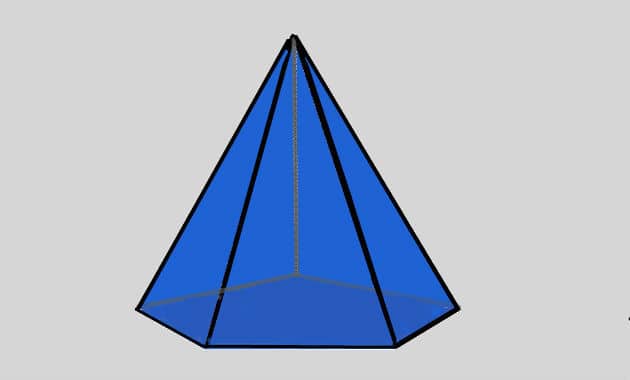
Pirámide
Las pirámides son sólidos geométricos formados por una base poligonal y un vértice (vértice de la pirámide) que une todas las caras laterales triangulares.
El número de lados del polígono base corresponde al número de caras laterales de la pirámide.
Obtenga más información sobre el tema:
Curiosidad
Al estudiar los poliedros regulares, el filósofo y matemático griego Platón relacionó cada uno de ellos con los elementos de la naturaleza: tetraedro (fuego), hexaedro (tierra), octaedro (aire), dodecaedro (universo) e icosaedro (agua).
Ejercicios resueltos
1) Enem – 2018
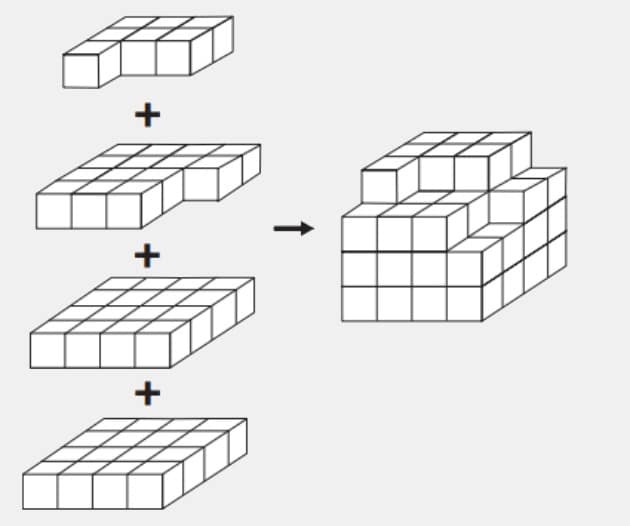
Minecraft es un juego virtual que puede ayudar en el desarrollo de conocimientos relacionados con el espacio y la forma. Es posible crear casas, edificios, monumentos e incluso naves espaciales, todo a escala real, mediante el apilamiento de cubos.
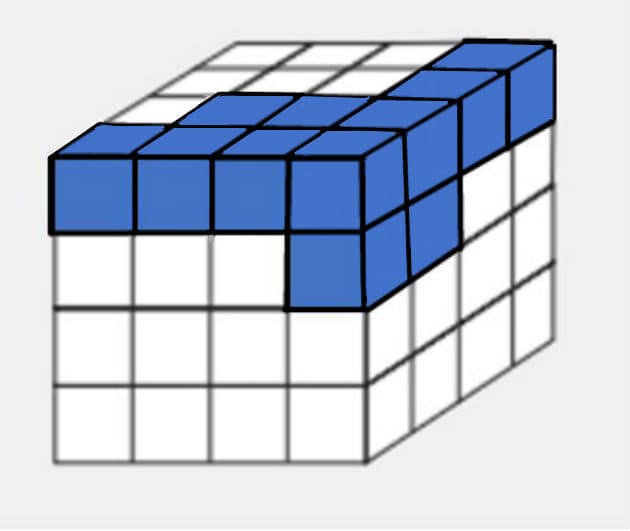
Un jugador quiere construir un cubo de 4 x 4 x 4. Ya ha apilado algunos de los cubos necesarios, como se muestra en la figura.
Los cubos que aún deben apilarse para terminar la construcción del cubo, juntos, forman una sola pieza, capaz de completar la tarea.
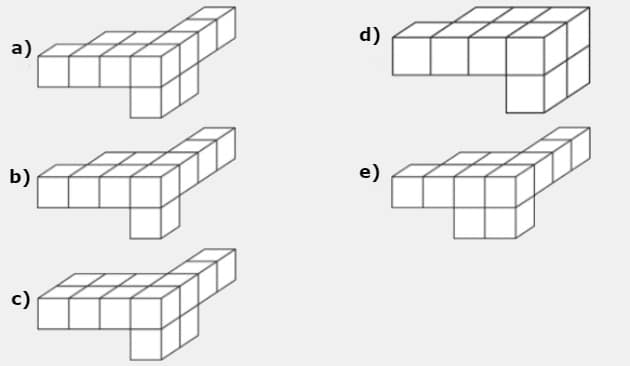
La forma de la pieza capaz de completar el cubo de 4 x 4 x 4 es
2) Enem – 2017
Una cadena de hoteles tiene cabañas simples en la isla de Gotland, Suecia, como se muestra en la Figura 1. La estructura de soporte de cada una de estas cabañas se muestra en la Figura 2. La idea es permitir que el huésped se mantenga libre de tecnología, pero conectado con la naturaleza.