Tabla de contenidos
Tú polígonos son figuras planas y cerradas formadas por segmentos de línea recta. La palabra «polígono» proviene del griego y constituye la unión de dos términos «escuela politécnica» y «vamos«que significa» muchos ángulos «.
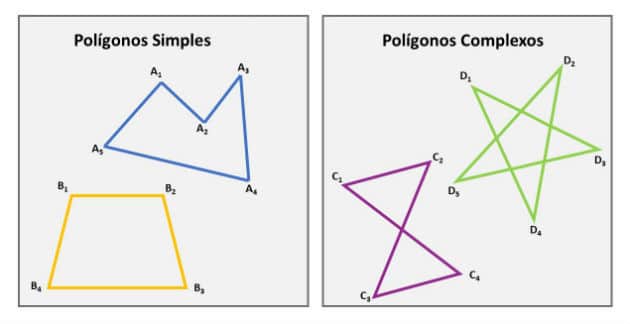
Los polígonos pueden ser simples o complejos. Los polígonos simples son aquellos cuyos segmentos consecutivos que los forman no son colineales, no se cruzan y se tocan solo en los extremos.
Cuando hay una intersección entre dos lados no consecutivos, el polígono se llama complejo.
Polígono convexo y cóncavo
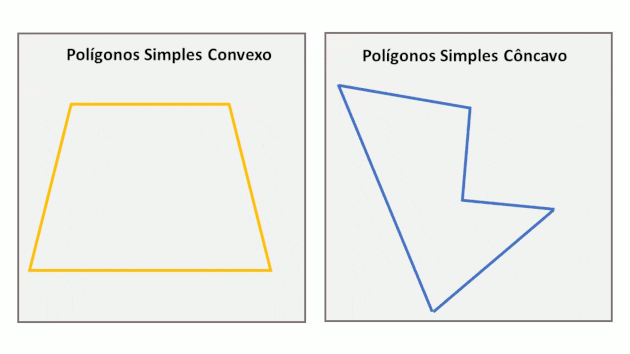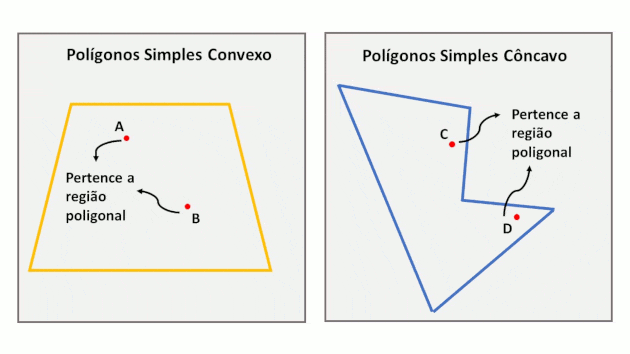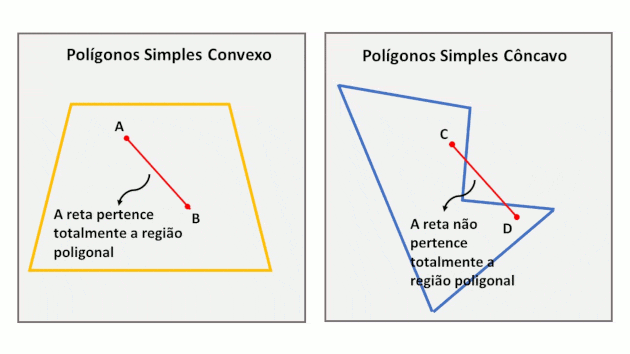
La unión de las líneas que forman los lados de un polígono con su interior se llama región poligonal. Esta región puede ser convexa o cóncava.
Los polígonos simples se denominan convexos cuando cualquier línea que une dos puntos, pertenecientes a la región poligonal, se insertará completamente en esta región. En el caso de polígonos cóncavos, esto no sucede.
Polígonos regulares
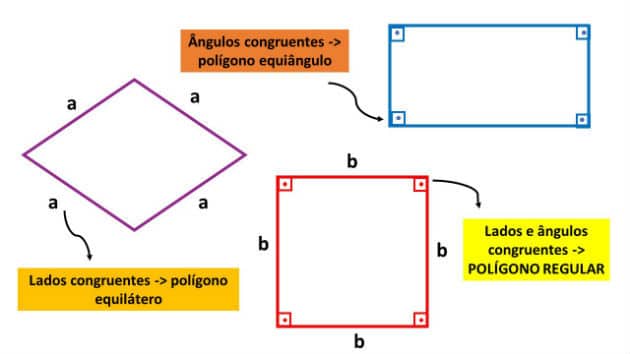
Cuando un polígono tiene todos los lados congruentes entre sí, es decir, tienen la misma medida, se llama equilátero. Cuando todos los ángulos tienen la misma medida, se llama equi-ángulo.
Los polígonos convexos son regulares cuando tienen lados y ángulos congruentes, es decir, son tanto equiláteros como equiangulares. Por ejemplo, el cuadrado es un polígono regular.
Elementos de polígono
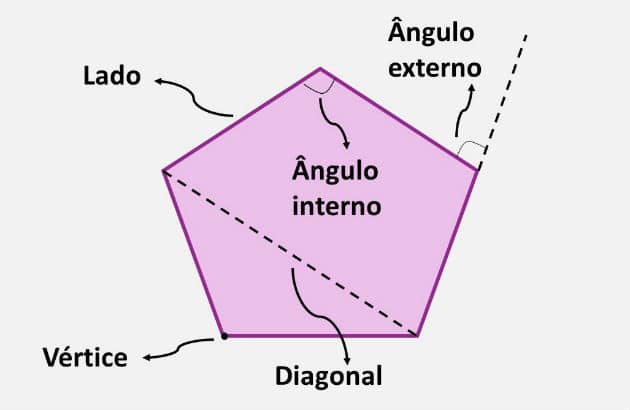
- Vértice: corresponde al punto de encuentro de los segmentos que forman el polígono.
- Lado: corresponde a cada segmento de línea que une vértices consecutivos.
- Anglos: usted ángulos internos corresponden a los ángulos formados por dos lados consecutivos. Por otro lado, ángulos externos son los ángulos formados por un lado y por la extensión del lado que lo sigue.
- Diagonal: corresponde al segmento de recta que conecta dos vértices no consecutivos, es decir, un segmento de recta que pasa por el interior de la figura.
Nomenclatura de polígono
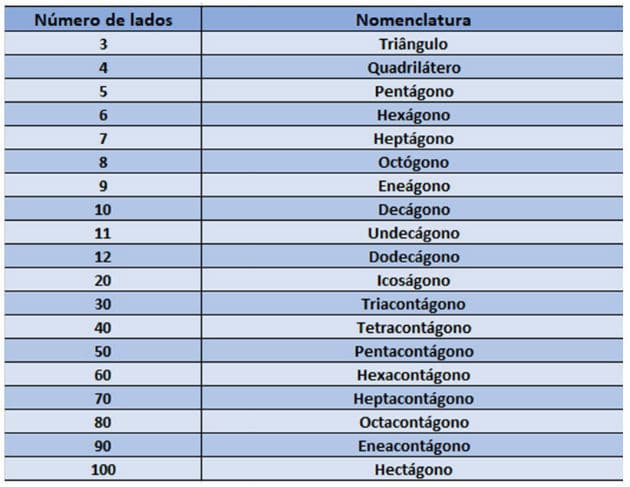
Dependiendo del número de lados presentes, los polígonos se clasifican en:
Obtenga más información sobre los cuadriláteros.
Suma de los ángulos de un polígono
La suma de los ángulos externos de los polígonos convexos es siempre igual a 360º. Sin embargo, para obtener la suma de los ángulos internos de un polígono es necesario aplicar la siguiente fórmula:
Ser:
norte: número de lados del polígono
Ejemplo
¿Cuál es la suma de los ángulos internos de un icoságono convexo?
Solución
El icoságono convexo es un polígono que tiene 20 lados, es decir n = 20. Aplicando este valor en la fórmula, tenemos:
Por tanto, la suma de los ángulos internos del icoságono es igual a 3240º.
Numero de diagonales
Para calcular el número de diagonales de un polígono, se utiliza la siguiente fórmula:
Ejemplo
¿Cuántas diagonales tiene un octágono convexo?
Solución
Considerando que el octágono tiene 8 lados, aplicando la fórmula tenemos:
Por lo tanto, un octágono convexo contiene 20 diagonales.
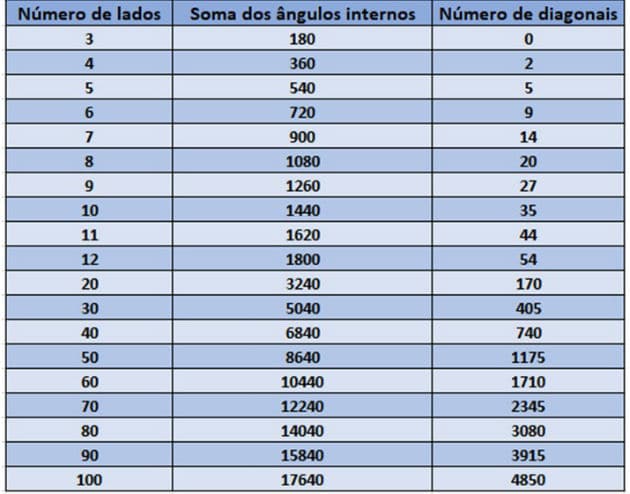
En la siguiente tabla, tenemos el valor de la suma de los ángulos internos y el número de diagonales de los polígonos convexos según el número de lados:
Perímetro y área de polígonos
El perímetro es la suma de las medidas de todos los lados de una figura. Así, para conocer el perímetro de un polígono, basta con sumar las medidas de los lados que lo componen.
El área se define como la medida de su superficie. Para encontrar el valor del área de un polígono, usamos fórmulas según el tipo de polígono.
Por ejemplo, el área del rectángulo se calcula multiplicando la medida del ancho por la longitud.
El área del triángulo es igual a la multiplicación de la base por la altura y el resultado se divide por 2.
Para aprender a calcular el área de otros polígonos, lea también:
Fórmula del área del polígono desde el perímetro
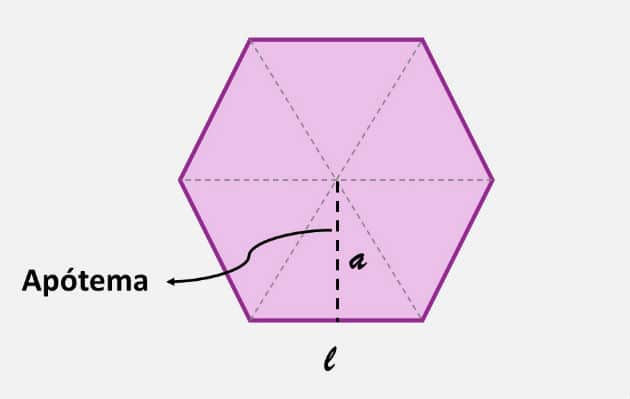
Cuando conocemos el valor del perímetro de un polígono regular, podemos usar la siguiente fórmula para calcular su área:
Ser:
PAG: semiperímetro (la medida del perímetro dividida por 2).
La: apótema
vea también: Área hexagonal
Ejercicios resueltos
1) CEFET / RJ – 2016
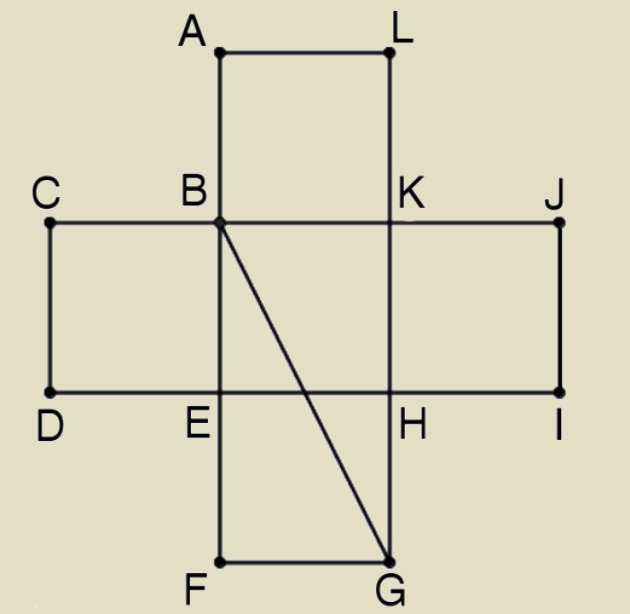
El patio trasero de la casa de Manoel está formado por cinco cuadrados ABKL, BCDE, BEHK, HIJK y EFGH, de la misma zona y tiene la forma de la figura en el lateral. Si BG = 20 m, entonces el área del patio es:
a) 20 mdos
b) 30 mdos
c) 40 mdos
d) 50 mdos
2) Faetec / RJ – 2015
Un polígono regular cuyo perímetro mide 30 cm tiene n lados, cada uno mide (n – 1) cm. Este polígono se clasifica como uno:
un triángulo
b) cuadrado
c) hexágono
d) heptágono
e) pentágono
Para obtener más información, lea también Formas geométricas y fórmulas matemáticas.