Tabla de contenidos
O volumen de la pirámide corresponde a la capacidad total de esta figura geométrica.
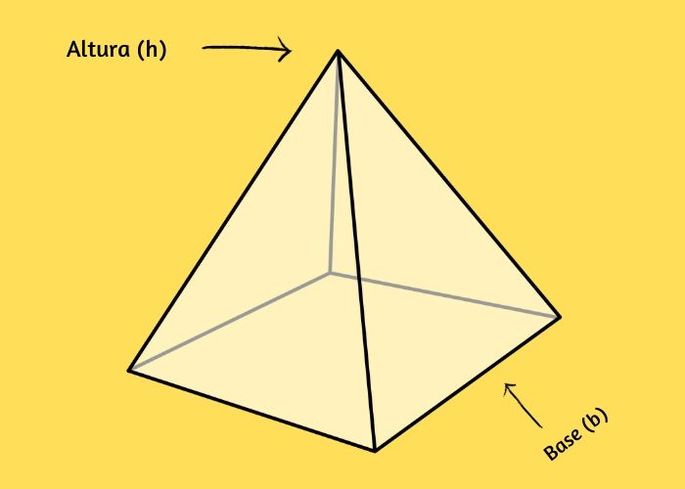
Recuerda que la pirámide es un sólido geométrico con base poligonal. El vértice de la pirámide representa el punto más alejado de su base.
Así, todos los vértices de esta figura están en el plano de la base. La altura de la pirámide se calcula por la distancia entre el vértice y su base.
En cuanto a la base, tenga en cuenta que puede ser triangular, pentagonal, cuadrada, rectangular o paralelogramo.
Fórmula piramidal
Para calcular el volumen de la pirámide se utiliza la siguiente fórmula:
- V = 1/3 AB.H
Dónde,
V: volumen de la pirámide
LAB: Área de la base
H: altura
1. Pirámide de base triangular
El cálculo del volumen de una pirámide triangular, también llamada tetraedro, se realiza calculando el área del triángulo (base) que se encuentra en el plano. Luego se multiplica por la altura y se divide por tres.
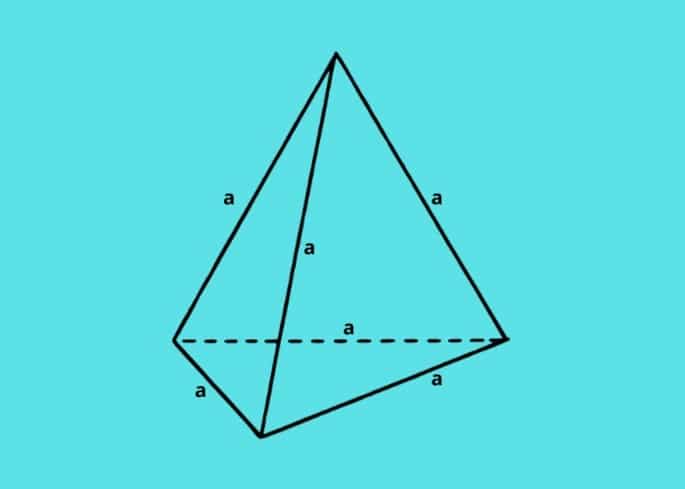
Siendo así:
2. Pirámide de base cuadrada
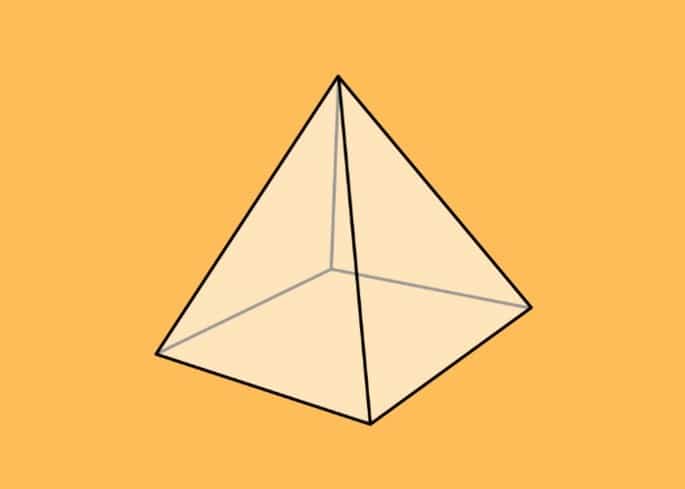
En una pirámide de base rectangular, el área del rectángulo (lado menor x lado mayor) se resuelve inicialmente, se multiplica por la altura y se divide por tres.
En el caso de una pirámide cuadrada, la base será un cuadrado y el área del cuadrado el lado del cuadrado (ldos).
Siendo así:
-
(Pirámide cuadrada)
-
(Pirámide rectangular)
3. Pirámide hexagonal
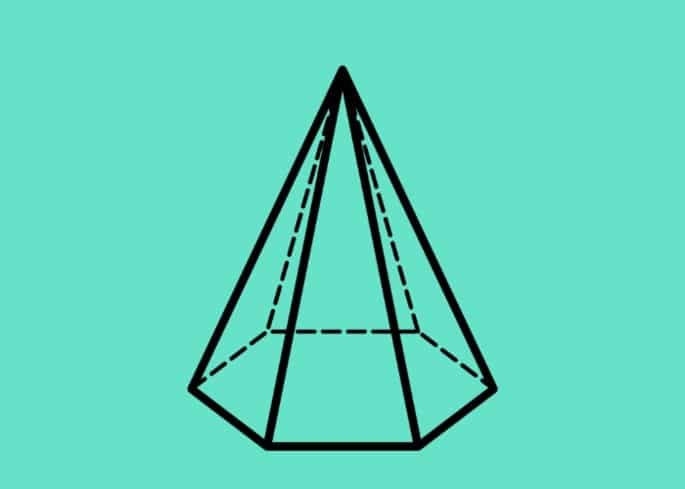
Asimismo, el volumen de la pirámide hexagonal comienza a resolverse a partir del área de su base. Recordando que la fórmula del área de un hexágono es:
Por tanto, la fórmula del volumen de la pirámide hexagonal se puede entender como:
Ejercicios resueltos
1. Determine el volumen de una pirámide hexagonal regular con una altura de 30 cm y un borde de base de 20 cm.
Resolución:
Primero, tenemos que encontrar el área en la base de esta pirámide. En este ejemplo, es un hexágono regular con un lado de l = 20 cm. Pronto,
LAB = 6. ldos√3 / 4
LAB = 6. 20dos√3 / 4
LAB = 600√3 cmdos
Hecho esto, podemos sustituir el valor del área base en la fórmula de volumen:
V = 1/3 AB.H
V = 1/3. 600√3. 30
V = 6000√3 cm3
dos. ¿Cuál es el volumen de una pirámide regular de 9 m de altura con una base cuadrada con un perímetro de 8 m?
Resolución:
Para solucionar este problema, tenemos que ser conscientes del concepto de perímetro. Es la suma de todos los lados de una figura. Como es un cuadrado, tenemos que cada lado mide 2 m de largo.
Entonces, podemos encontrar el área base:
LAB = 2dos = 4 m
Hecho esto, reemplacemos el valor en la fórmula del volumen de la pirámide:
V = 1/3 AB.H
V = 1/3 4. 9
V = 1/3. 36
V = 36/3
V = 12 m3
Ejercicios vestibulares con retroalimentación
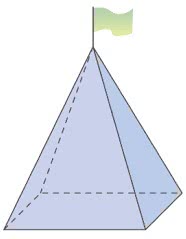
1. (Vunesp) El alcalde de una ciudad tiene la intención de colocar un asta de bandera frente al ayuntamiento, que se apoyará en una pirámide de base cuadrada hecha de concreto sólido, como se muestra en la figura.
Sabiendo que el borde de la base de la pirámide será de 3 my la altura de la pirámide será de 4 m, el volumen de hormigón (en m3) necesarios para la construcción de la pirámide serán:
a) 36
b) 27
c) 18
d) 12
e) 4
dos. (Unifor-CE) Una pirámide regular mide 6√3 cm de alto y el borde de la base mide 8 cm. Si los ángulos internos de la base y todas las caras laterales de esta pirámide suman 1800 °, su volumen, en centímetros cúbicos, es:
a) 576
b) 576√3
c) 1728
d) 1728√3
e) 3456
3. (UNIRIO-RJ) Los bordes laterales de una pirámide recta miden 15 cm, y su base es un cuadrado cuyos lados miden 18 cm. La altura de esta pirámide, en cm, es igual a:
a) 2√7
b) 3√7
c) 4√7
d) 5√7
Lea mas: