Los polinomios son expresiones algebraicas formadas por números (coeficientes) y letras (partes literales). Las letras de un polinomio representan los valores desconocidos de la expresión.
EJEMPLOS
a) 3ab + 5
b) x3 + 4xy – 2xdosy3
c) 25 vecesdos – 9 añosdos
Monomial, Binomial y Trinomial
Los polinomios están formados por términos. La única operación entre los elementos de un término es la multiplicación.
Cuando un polinomio tiene solo un término, se llama monomio.
EJEMPLOS
a) 3 veces
b) 5abc
c) xdosy3z4
La llamada binomios son polinomios que tienen solo dos monomios (dos términos), separados por una operación de suma o resta.
EJEMPLOS
a) eldos – Bdos
b) 3x + y
c) 5ab + 3cddos
La trinomios son polinomios que tienen tres monomios (tres términos), separados por operaciones de suma o resta.
Ejemplos
a) xdos + 3x + 7
b) 3ab – 4xy – 10 años
cm3n + mdos + n4
Grado de polinomios
El grado de un polinomio viene dado por los exponentes de la parte literal.
Para encontrar el grado de un polinomio, debemos sumar los exponentes de las letras que componen cada término. La mayor suma será el grado del polinomio.
EJEMPLOS
a) 2x3 + y
El exponente del primer término es 3 y el segundo término es 1. Dado que el mayor es 3, el grado del polinomio es 3.
b) 4 xdosy + 8x3y3 – xy4
Agreguemos los exponentes de cada término:
4xdosy => 2 + 1 = 3
8x3y3 => 3 + 3 = 6
xy4 => 1 + 4 = 5
Dado que la suma más grande es 6, el grado del polinomio es 6
Nota: el polinomio nulo es aquel que tiene todos los coeficientes iguales a cero. Cuando esto ocurre, el grado del polinomio no está definido.
Operaciones con polinomios
Consulte los siguientes ejemplos de operaciones entre polinomios:
Agregar polinomios
Hacemos esto sumando los coeficientes de términos similares (la misma parte literal).
(- 7x3 + 5 xdosy – xy + 4y) + (- 2xdosy + 8xy – 7y)
– 7x3 + 5 vecesdosy – 2xdosy – xy + 8xy + 4y – 7y
– 7x3 + 3 vecesdosaños + 7xy – 3 años
Restar polinomios
El signo menos delante del paréntesis invierte los signos dentro del paréntesis. Después de eliminar los paréntesis, debemos agregar términos similares.
(4 vecesdos – 5xk + 6k) – (3x – 8k)
4xdos – 5xk + 6k – 3xk + 8k
4xdos – 8xk + 14k
Multiplicar polinomios
En la multiplicación, debemos multiplicar término por término. En la multiplicación de letras iguales, los exponentes se repiten y se suman.
(3 vecesdos – 5x + 8). (-2x + 1)
-6x3 + 3 vecesdos + 10 vecesdos – 5x – 16x + 8
-6x3 + 13xdos – 21x +8
División de polinomios
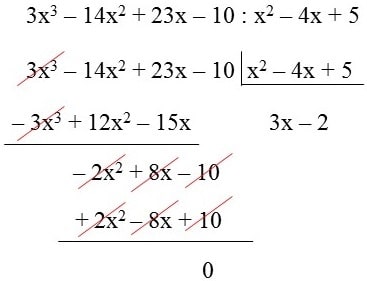
Nota: En la división de polinomios usamos el método clave. Primero, dividimos los coeficientes numéricos y luego dividimos las potencias de la misma base. Para hacer esto, mantén la base y resta los exponentes.
Factorización de polinomios
Para realizar la factorización de polinomios tenemos los siguientes casos:
Factor común en la evidencia
ax + bx = x (a + b)
Ejemplo
4x + 20 = 4 (x + 5)
Agrupamiento
ax + bx + ay + por = x. (a + b) + y. (a + b) = (x + y). (a + b)
Ejemplo
8ax + bx + 8ay + por = x (8a + b) + y (8a + b) = (8a + b). (x + y)
Trinomio cuadrado perfecto (suma)
Lados + 2ab + bdos = (a + b)dos
Ejemplo
Xdos + 6x + 9 = (x + 3)dos
Trinomio cuadrado perfecto (diferencia)
Lados – 2ab + bdos = (a – b)dos
Ejemplo
Xdos – 2x + 1 = (x – 1)dos
Diferencia de dos cuadrados
(a + b). (a – b) = ados – Bdos
Ejemplo
Xdos – 25 = (x + 5). (x – 5)
Cubo perfecto (adición)
La3 + 3adosb + 3abdos + b3 = (a + b)3
Ejemplo
X3 + 6xdos + 12x + 8 = x3 + 3. Xdos . 2 + 3. X. dosdos + 23 = (x + 2)3
Cubo perfecto (diferencia)
La3 – 3ºdosb + 3abdos – B3 = (a – b)3
Ejemplo
y3 – 9 añosdos + 27 años – 27 = años3 – 3. ydos . 3 + 3. y. 3dos – 33 = (y – 3)3
Lea también:
Ejercicios resueltos
1) Clasifique los siguientes polinomios en monomios, binomios y trinomios:
a) 3abcddos
b) 3a + bc – ddos
c) 3ab – cddos
2) Indique el grado de los polinomios:
a) xy3 + 8xy + xdosy
b) 2x4 + 3
c) ab + 2b + a
d) zk7 – 10zdosk3w6 + 2x
3) ¿Cuál es el valor del perímetro de la siguiente figura?

4) Encuentra el área de la figura:

5) Factoriza los polinomios
a) 8ab + 2adosb – 4abdos
b) 25 + 10 años + añosdos
c) 9 – kdos
Ver también: Expresiones algebraicas y ejercicios sobre expresiones algebraicas