El triángulo isósceles es un polígono que tiene tres lados, dos de los cuales son congruentes (la misma medida).
El lado con una medida diferente se llama la base del triángulo isósceles. El ángulo formado por los dos lados congruentes se llama ángulo de vértice.
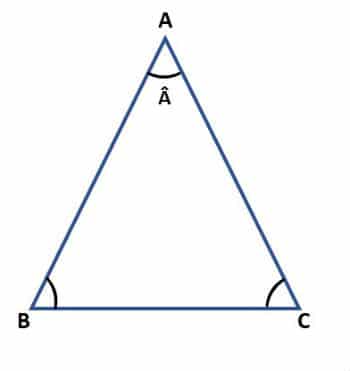
En el triángulo isósceles ABC, que se muestra a continuación, los lados tienen la misma medida. El lado
es la base del triángulo. El punto A es el vértice, mientras que el ángulo
es el ángulo del vértice.
Propiedades de los triángulos isósceles
Todo triángulo isósceles tiene las siguientes propiedades:
- Los ángulos de la base son congruentes;
- La bisectriz del ángulo del vértice coincide con la altura relativa a la base y la mediana.
Para probar estas propiedades, usaremos un triángulo isósceles ABC. Trazando la bisectriz del ángulo del vértice, formamos los triángulos ABM y ACM, como se muestra en la siguiente figura:
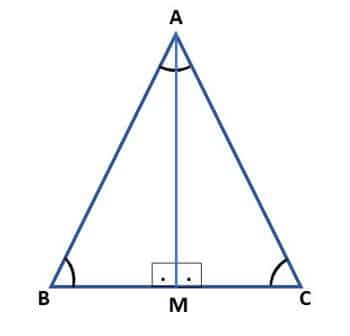
Tenga en cuenta que el lado es común a los dos triángulos y la bisectriz dividió el ángulo
en dos ángulos de la misma medida. Además, los lados
son congruentes (lados iguales del triángulo isósceles ABC).
De esta forma, tenemos el caso de congruencia de triángulos LAL (lado, ángulo, lado). Luego concluimos que los ángulos , en la base del triángulo, tienen la misma medida.
También podemos concluir que, dado que los triángulos ABM y ACM son congruentes, la medida son iguales.
Por lo tanto, también es la mediana en relación con la base. Además,
también es la altura relativa a la base, ya que forma dos ángulos iguales a 90º con la base.
Área de triángulos
Para encontrar el área de un triángulo isósceles usamos la fórmula del área de cualquier triángulo:
Dónde:
La zona
b: medida de la base
h: medida de altura relativa a la base
Ejemplo:
¿Cuál es el valor del área de un triángulo isósceles que tiene lados iguales a 10 cm, 10 cm y 12 cm?
La base del triángulo mide 12 cm, sin embargo, no tenemos la medida de la altura. Sin embargo, sabemos que coincide con la mediana. De esta forma la altura dividirá la base en dos segmentos iguales, es decir, 12: 2 = 6.
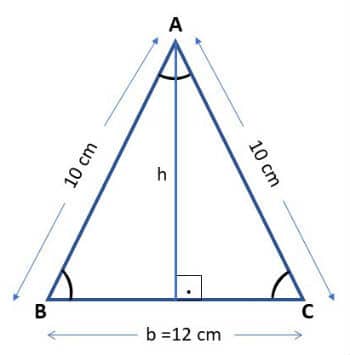
Para encontrar la altura usaremos el teorema de Pitágoras:
10dos = 6dos + hdos
Hdos = 100 – 36
Hdos = 64
h = 8 cm
Ahora, podemos calcular el área:
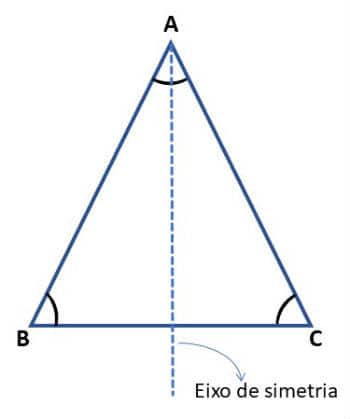
Eje de simetria
El eje de simetría de una figura es una línea recta que la divide en otras dos figuras idénticas y que cuando doblamos a lo largo del eje de simetría, estas figuras se superponen perfectamente.
Los triángulos isósceles tienen solo 1 eje de simetría, que es la línea que divide el ángulo del vértice en dos ángulos iguales (bisectriz).
Clasificación de triángulos
Además de los triángulos isósceles, también tenemos los triángulos equilátero y escaleno. Esta clasificación tiene en cuenta los lados que forman el triángulo.
Así, el triángulo equilátero es aquel que tiene tres lados con la misma medida y el escaleno todos los lados tienen medidas diferentes.

También podemos clasificar los triángulos en relación con los ángulos internos. El triángulo será agudo cuando la medida de los ángulos internos sea menor a 90º.
Cuando el triángulo tenga un ángulo recto (igual a 90º) se clasificará como triángulo rectángulo y ángulo obtuso cuando tenga un ángulo mayor a 90º.
