Poliedros – Geometría espacial – Matemáticas
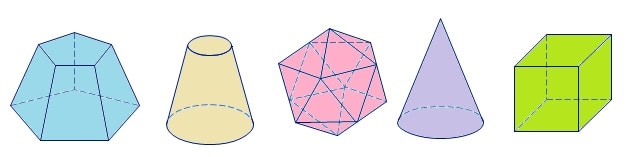
En geometría espacial, las formas tridimensionales se denominan sólidos geométricos. Algunos ejemplos: Podemos dividir los sólidos geométricos más simples en dos tipos: Poliedros Son aquellos …
Geometría espacial: todo lo que importa
La Geometría espacial Corresponde al área de las matemáticas encargada de estudiar las figuras en el espacio, es decir, aquellas con más de dos dimensiones. En …
Formas geométricas
Las formas geométricas son las formas de las cosas que observamos y están formadas por un conjunto de puntos. La geometría es el área de …
Área y perímetro: todo lo que importa
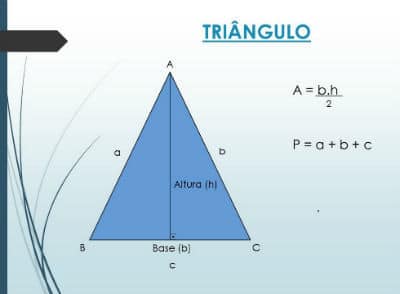
En geometría, los conceptos de área y perímetro se utilizan para determinar las medidas de alguna figura. Vea a continuación el significado de cada concepto: …
Área del trapecio: cálculo del área del trapecio
El área del trapecio mide el valor de la superficie de esta figura plana formada por cuatro lados. El trapecio es un cuadrilátero que tiene …
Relaciones trigonométricas
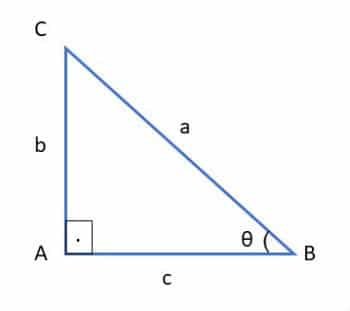
Las relaciones trigonométricas son relaciones entre valores de las funciones trigonométricas del mismo arco. Estas relaciones también se denominan identidades trigonométricas. Inicialmente, la trigonometría tenía …
Poliedro – Toda la materia
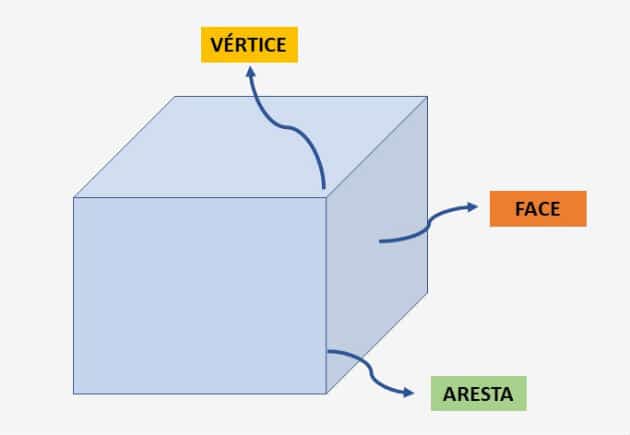
Los poliedros son sólidos geométricos limitados por un número finito de polígonos planos. Estos polígonos forman las caras del poliedro. La intersección de dos caras …
Polígonos: toda la materia
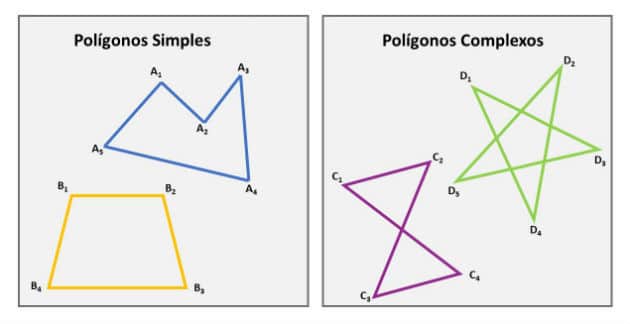
definición Matemáticas › Geometría Tú polígonos son figuras planas y cerradas formadas por segmentos de línea recta. La palabra «polígono» proviene del griego y constituye …
Cuadrado perfecto: que es, como calcular, ejemplos y reglas
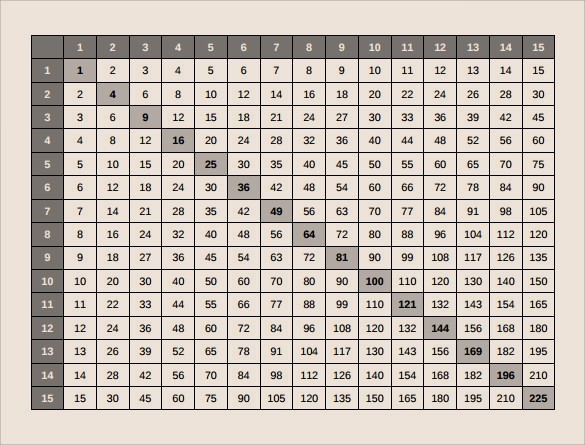
Un cuadrado perfecto o un número cuadrado perfecto es un número natural que, si tiene raíz, da como resultado otro número natural. Es decir, son …
Cuadriláteros: toda la materia
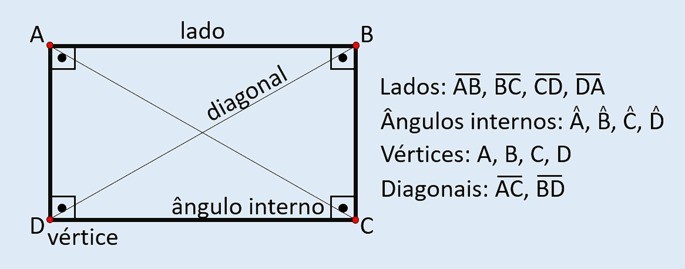
definición Matemáticas › Geometría El cuadrilátero es un polígono que tiene cuatro lados. Esta figura geométrica bidimensional está formada por: Lados: son los segmentos de …
