LA trigonometría es la parte de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos.
También se utiliza en otras áreas de estudio como física, química, biología, geografía, astronomía, medicina, ingeniería, etc.
Funciones trigonométricas
Las funciones trigonométricas son funciones relacionadas con triángulos rectángulos, que tienen un ángulo de 90 °. Son: seno, coseno y tangente.
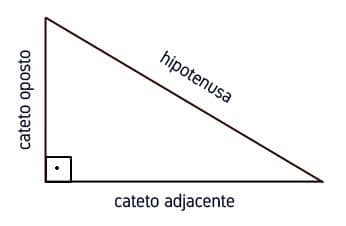
Las funciones trigonométricas se basan en las relaciones entre dos lados del triángulo en función de un ángulo.
Están formados por dos lados (opuesto y adyacente) y la hipotenusa:
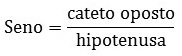
El lado opuesto se lee sobre la hipotenusa.
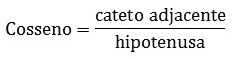
Se lee el tramo adyacente a la hipotenusa.
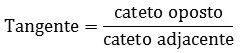
El lado opuesto se lee sobre el lado adyacente.
Lea mas:
Círculo trigonométrico
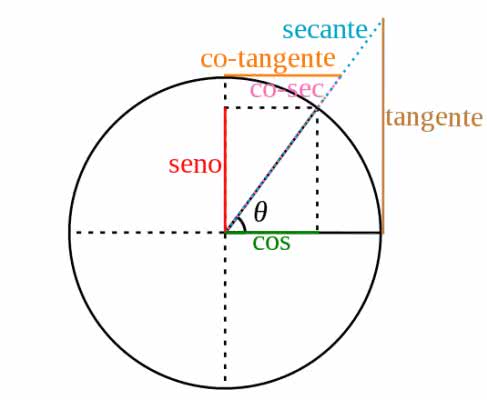
El círculo trigonométrico o círculo unitario se utiliza en el estudio de funciones trigonométricas: seno, coseno y tangente.
Teoría Euclidiana
Algunos conceptos importantes de la geometría euclidiana en los estudios de trigonometría son:
Ley del Senado
La Ley de Senos establece que en un triángulo dado, la razón entre el valor de un lado y el seno de su ángulo opuesto, siempre será constante.
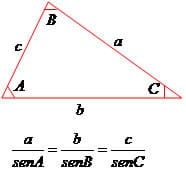
Así, para un triángulo ABC de lados a, b, c, la Ley de Senos está representada por la siguiente fórmula:
Ley de los cosenos
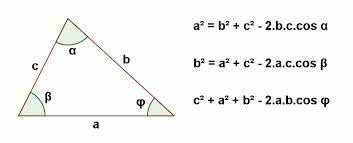
La Ley de los cosenos establece que en cualquier triángulo, el cuadrado de un lado corresponde a la suma de los cuadrados de los otros dos lados, menos el doble del producto de esos dos lados por el coseno del ángulo entre ellos.
De esta forma, su fórmula se representa de la siguiente manera:
Ley de las tangentes
LA Ley de las tangentes establece la relación entre las tangentes de dos ángulos de un triángulo y las longitudes de sus lados opuestos.
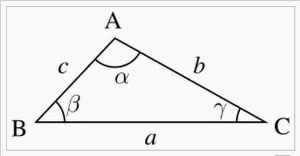
Así, para un triángulo ABC, con lados a, b, c, y ángulos α, β y γ, opuestos a estos tres lados, tenemos la expresión:
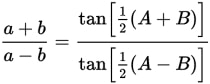
Teorema de pitágoras
El Teorema de Pitágoras, creado por el filósofo y matemático griego Pitágoras de Samos (570 aC – 495 aC), se usa ampliamente en estudios trigonométricos.
Demuestra que en el triángulo rectángulo, compuesto por un ángulo interno de 90 ° (ángulo recto), la suma de los cuadrados de sus lados corresponde al cuadrado de su hipotenusa:
Lados = cdos+ bdos
Ser,
La: hipotenusa
C y B: coleccionistas

Lea también: Trigonometría en el triángulo rectángulo.
Historia de la trigonometría
La historia de la trigonometría surge a medida que los astrónomos necesitaban calcular el tiempo, y también es muy importante en la investigación sobre navegación.
Sin emabargo, Hiparco de Nicea, (190 a. C.-120 a. C.), astrónomo greco-otomano, fue quien introdujo la trigonometría en los estudios científicos. Por esta razón, se le considera el fundador o el padre de la trigonometría.
Curiosidad
El término «trigonometría», del griego, es la unión de las palabras trígono (triángulo) y metro (medidas).
Ejercicios vestibulares de trigonometría
1. (UFAM) Si el cateto y la hipotenusa de un triángulo rectángulo miden 2a y 4a, respectivamente, entonces la tangente del ángulo opuesto al lado más corto es:
a) 2√3
b) √3 / 3
c) √3 / 6
d) √20 / 20
e) 3√3
dos. (Cesgranrio) Una rampa plana, de 36 m de largo, forma un ángulo de 30 ° con el plano horizontal. Una persona que sube toda la rampa se eleva verticalmente desde:
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
3. (Unicamp) La hipotenusa de un triángulo rectángulo mide 1 metro y uno de los ángulos agudos es el triple del otro.
a) Calcula las longitudes de los catetos.
b) Muestre que la longitud del cateto más grande está entre 92 y 93 centímetros.