El hexágono es un polígono que tiene seis lados delimitados por segmentos de línea. Esta figura plana está formada por la unión de seis triángulos equiláteros.
Cuando el hexágono es regular, todos los lados tienen la misma medida y sus ángulos internos son 120º. Por lo tanto, el área del hexágono es seis veces el área de un triángulo equilátero que lo compone.
¿Cómo calcular el área del hexágono regular?
La fórmula para calcular el área del hexágono es:
A continuación se muestran los pasos para llegar a esta fórmula.
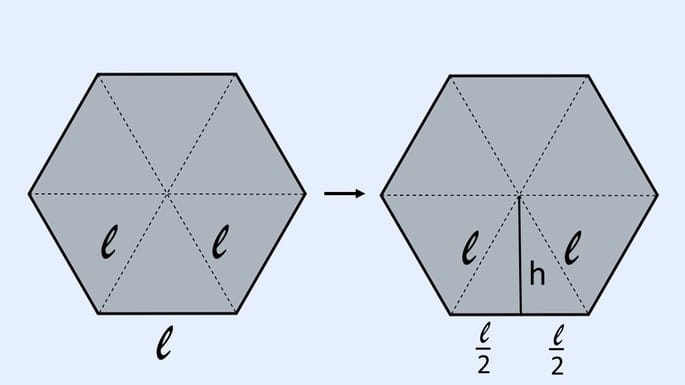
El triángulo equilátero tiene tres lados de la misma medida. Cuando dibujamos una línea, que representa la altura (h), dividimos un triángulo equilátero en otros dos triángulos.
Aplicando el Teorema de Pitágoras, encontramos la altura del triángulo de la siguiente manera:
La fórmula para calcular el área del triángulo es:
Reemplazando los términos, tenemos:
Dado que el hexágono está formado por seis triángulos equiláteros, el área del hexágono es seis veces el área del triángulo. Vea:
Ejercicio resuelto: Para hacer un hexágono, Pedro cortó cartulina y con una regla midió que todos los lados tuvieran 10 cm. ¿Cuál es el área del hexágono que creó Peter?
Usted también podría estar interesado en:
Cómo calcular el área de un hexágono a partir de la apotema.
Otra forma de calcular el área de un hexágono es usar el perímetro y la apotema. La fórmula utilizada es:
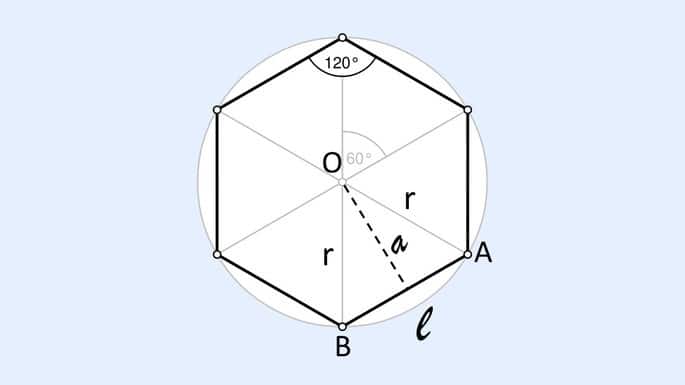
El perímetro (p) corresponde a la suma de los lados del polígono, mientras que la apotema () se encuentra trazando una línea entre el centro del hexágono y el punto medio de un lado de la figura.
Cuando se inscribe un hexágono regular en un círculo, los seis vértices de la figura dividen el círculo en seis partes iguales. En este caso, el radio del círculo (r) coincide con el lado del hexágono (l), ya que forman un triángulo equilátero. .
Ser , aplicamos el Teorema de Pitágoras y encontramos la fórmula para calcular el apotema de la siguiente manera:
Ejercicio resuelto: Sobre una circunferencia, cuyo radio mide 10 cm, se dibujó un hexágono regular. Calcule las medidas de lado, apotema y área del polígono dibujado.
Comprueba cómo calcular el área de otras figuras planas.: