Matemáticas

Triángulo de Pascal – definición

Written by admin

Triángulo de Pascal es un triángulo aritmético infinito donde se ordenan los coeficientes de expansiones binomiales. Los números que forman el triángulo tienen diferentes propiedades y relaciones.

Esta representación geométrica fue estudiada por el matemático chino Yang Hui (1238-1298) y por muchos otros matemáticos.

¿Eres estudiante, profesor o academia?

DATE DE ALTA EN NUESTRA RED SOCIAL!, Grupos de estudio, apuntes, escribe en tu propio blog, añadir tu academia o dar clases particulares y Aprende!!!.

Abrir un perfil

Sin embargo, los estudios más famosos fueron los del matemático italiano Niccolò Fontana Tartaglia (1499-1559) y el matemático francés Blaise Pascal (1623-1662).

Ya que Pascal estudió el triángulo aritmético más profundamente y demostró varias de sus propiedades.

En la antigüedad, este triángulo se utilizó para calcular algunas raíces. Más recientemente, se utiliza en el cálculo de probabilidades.

Además, los términos del binomio de Newton y la secuencia de Fibonacci se pueden encontrar a partir de los números que forman el triángulo.

Coeficiente binomial

Los números que componen el triángulo de Pascal se denominan números binomiales o coeficientes binomiales. Un número binomial está representado por:

abrir la línea de la tabla entre paréntesis con n línea con p al final de la tabla cerrar paréntesis

Con norte y PAG números naturales yn ≥ p. El número norte se llama numerador y el PAG denominador.

El número binomial se calcula a partir de la relación:

abrir paréntesis línea de tabla con n línea con p final de tabla cerrar paréntesis igual a C con n coma p subíndice final de subíndice igual al numerador n factorial sobre denominador p factorial paréntesis izquierdo n menos p paréntesis derecho final factorial de fracción

Ser,

Cn, p: combinación simple de n elementos tomados pap
n!: factorial de n, es decir, n. (n – 1). (n – 2) … 3.2.1
p!: factorial de p, es decir, p. (p – 1). (p – 2) … 3.2.1

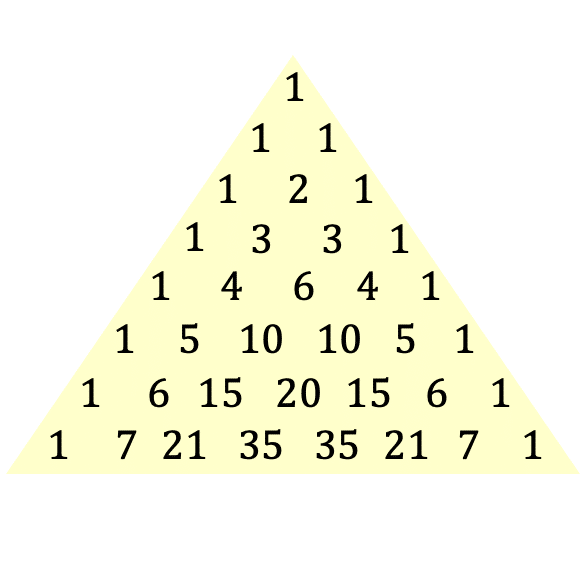
Construcción del Triángulo

El triángulo de Pascal se construye colocando los números binomiales del mismo numerador en la misma línea y los coeficientes del mismo denominador en la misma columna. Así tenemos:

espacio línea 0 espacio espacio espacio espacio espacio espacio espacio espacio abre paréntesis línea de tabla con 0 línea con 0 final de tabla cierra paréntesis espacio de línea 1 espacio espacio espacio espacio espacio espacio espacio abre paréntesis línea de tabla con 1 línea con 0 final de tabla cierra paréntesis espacio abre paréntesis tabla fila con 1 fila con 1 extremo de la tabla cierra paréntesis espacio de fila 2 espacio espacio espacio espacio espacio espacio espacio espacio abre paréntesis fila de tabla con 2 línea con 0 final de la tabla cierra paréntesis espacio abre paréntesis línea de tabla con 2 fila con 1 final de la mesa cerrar paréntesis espacio abrir paréntesis línea de la tabla con 2 líneas con 2 final de la mesa cerrar paréntesis espacio de línea 3 espacio espacio espacio espacio espacio espacio espacio espacio espacio abierto paréntesis línea de la tabla con 3 línea con 0 final de la mesa cerrar paréntesis espacio abrir paréntesis línea de la tabla con 3 la línea con 1 final de la tabla cierra el espacio entre paréntesis abre la fila de la tabla con 3 filas con 2 finales de la tabla cierra el espacio entre paréntesis fila de tabla de paréntesis abierta con 3 filas con extremo de tabla 3 cerrar espacio de paréntesis espacio de línea espacio de 4 espacio espacio espacio espacio espacio espacio espacio de paréntesis abierto línea de tabla con 4 líneas con 0 final de la tabla cerrar espacio de paréntesis espacio abierto de paréntesis línea de tabla con 4 líneas con 1 extremo de la tabla cierra paréntesis espacio abre paréntesis fila de tabla con 4 filas con 2 extremos de la tabla cierra paréntesis espacio abre paréntesis fila de tabla con 4 filas con 3 extremos de la tabla cierra paréntesis espacio abre paréntesis fila de tabla con 4 filas con 4 extremos de la tabla tabla cierra paréntesis espacio espacio espacio espacio elipsis vertical línea espacio n espacio espacio espacio espacio espacio espacio espacio espacio espacio abre paréntesis línea de tabla con n línea con 0 final de tabla cierra paréntesis espacio abre paréntesis línea de tabla con n línea con 1 final de tabla cierra paréntesis espacio abre la línea de la tabla entre paréntesis con n línea con 2 al final de la tabla cierra el espacio entre paréntesis abre la línea de la tabla entre paréntesis con n línea con 3 al final de la pestaña cierra el espacio entre paréntesis abre la línea de la tabla entre paréntesis con n línea con 4 al final de la tabla cierra el paréntesis ... abre la línea de la tabla entre paréntesis con n línea con n al final de la tabla cierra el espacio entre paréntesis

Al calcular los valores de los coeficientes, encontramos la siguiente representación del triángulo de Pascal:

Triángulo de Pascal

propiedades

1º) Todas las líneas tienen el número 1 como primer y último elemento..

De hecho, el primer elemento de todas las líneas se calcula mediante:

abrir paréntesis línea de tabla con n línea con 0 final de tabla cerrar paréntesis igual al numerador n factorial sobre denominador 0 factorial paréntesis izquierdo n menos 0 paréntesis derecho factorial final de fracción igual al numerador n factorial sobre denominador 0 factorial n factorial final de fracción igual a 1 espacio espacio espacio espacio espacio espacio espacio espacio paréntesis izquierdo considerando espacio 0 factorial igual a 1 paréntesis derecho

y el último elemento de todas las líneas se calcula mediante:

abrir paréntesis línea de tabla con n línea con n final de tabla cerrar paréntesis igual al numerador n factorial sobre denominador n final factorial de fracción igual a 1

2do) El resto de los números de una línea se forman sumando los dos números más cercanos a la línea de arriba.

Esta propiedad se denomina Relación de Stifel y se expresa mediante:

abrir paréntesis fila de tabla con celda con n menos 1 final de línea de celda con celda menos 1 final de celda final de tabla cerrar paréntesis más abrir paréntesis fila de tabla con celda con n menos 1 final de línea de celda con p final de tabla cerrar paréntesis igual a abrir la fila de la tabla entre paréntesis con n filas con p al final de la tabla cerrar paréntesis

Es posible verificar la relación de Stifel directamente en el triángulo de Pascal, porque a partir de la segunda línea, cada elemento es igual a la suma del elemento anterior con su anterior.

Construcción del triángulo de Pascal

3º) Los elementos de la misma línea equidistantes de los extremos tienen valores iguales.

abrir paréntesis línea de tabla con n línea con p fin de tabla cerrar paréntesis igual a abrir paréntesis línea de tabla con n línea con celda con n menos p fin de celda fin de tabla cerrar paréntesis flecha derecha p más paréntesis izquierdo n menos p paréntesis derecho igual a espacio espacio espacio paréntesis izquierdo números espacio binomial espacio espacio complementario paréntesis derecho

EJEMPLOS

La) fila de tabla de paréntesis abierta con 4 filas con 1 final de tabla cerrar paréntesis igual a fila de tabla de paréntesis abierta con 4 filas con 3 final de tabla cerrar paréntesis flecha derecha 1 más 3 igual a 4

B) fila de tabla con paréntesis abierto con 6 filas con 2 extremos de la tabla cerrar paréntesis igual a fila de tabla con paréntesis abierto con 6 filas con 4 extremos de tabla cerrar paréntesis flecha derecha 2 más 4 igual a 6

Cuarto) La suma de los elementos de una línea de numerador (n) será igual a 2norte.

Observe la siguiente tabla:

Tabla del triángulo de Pascal

Binomio de Newton

El binomio de Newton es la potencia de la forma (x + y)norte, ser X y y números reales y norte un número natural. Para pequeños valores de norte la expansión del binomio se puede hacer multiplicando sus factores.

Sin embargo, para exponentes más grandes, este método puede resultar muy laborioso. Por lo tanto, podemos usar el triángulo de Pascal para determinar los coeficientes binomiales de esta expansión.

Podemos representar la expansión del binomio (x + y)norte, como:

paréntesis izquierdo x más y paréntesis derecho elevado a la potencia de n igual a paréntesis abierto línea de tabla con n línea con 0 final de la tabla cierra paréntesis x elevado a n más abre paréntesis línea de tabla con n línea con 1 extremo de la tabla se cierra paréntesis x elevado a n menos 1 final de exponencial y más abre paréntesis línea de tabla con n línea con 2 final de tabla cierra paréntesis x elevado a la potencia de n menos 2 final de exponencial y al cuadrado más ... más abre paréntesis línea de tabla con n línea con k final de la tabla cierra paréntesis x elevado a la potencia de n menos k final de la exponencial y elevado a la potencia de k más ... más abre paréntesis fila de tabla con n fila con n final de tabla cierra paréntesis y al poder de n

Tenga en cuenta que los coeficientes de expansión corresponden a números binomiales, y estos números son los que forman el triángulo de Pascal.

Entonces, para determinar los coeficientes de expansión (x + y)norte , debemos considerar la línea norte correspondiente al triángulo de Pascal.

Ejemplo

Desarrollar el binomio (x + 3)6:

Solución:

Como el exponente del binomio es igual a 6, usaremos los números relacionados con la sexta línea del triángulo de Pascal para los coeficientes de esta expansión. Así tenemos:

Sexta línea del triángulo de Pascal: 1 6 15 20 15 6 1

Estos números serán los coeficientes de desarrollo del binomio.

(x + 3)6 = 1. X6. 30 + 6. X5. 31+15. X4. 3dos + 20. X3. 33 + 15. Xdos. 34 + 6. X1. 35+1. X0. 36

Resolviendo las operaciones encontramos la expansión del binomio:

(x + 3)6 = x6 +18. X5 +135 x4 + 540x3 + 1215 xdos + 1458 x + 729

Para obtener más información, lea también:

Ejercicios resueltos

1) Determine el séptimo término del desarrollo de (x + 1)9.

2) Calcula el valor de las siguientes expresiones, usando las propiedades del triángulo de Pascal.

el espacio entre paréntesis derecho abre paréntesis fila de la tabla con 4 filas con 0 final de la tabla cierra paréntesis más abre paréntesis fila de la tabla con 4 filas con 1 extremo de la tabla cierra paréntesis más abre paréntesis fila de la tabla con 4 filas con 2 extremos de la tabla cierra paréntesis más abre paréntesis fila de la tabla con 4 filas con 3 extremos de la tabla cierra paréntesis más abre paréntesis fila de la tabla con 4 filas con 4 extremos de la tabla cierra paréntesis

b espacio entre paréntesis a la derecha fila de tabla de paréntesis abierto con 6 filas con 4 extremos de la tabla cerrar paréntesis más fila de tabla de paréntesis abierta con 6 filas con 2 extremos de tabla cerrar paréntesis

c espacio entre paréntesis a la derecha fila de tabla con paréntesis abierto con 7 filas con 3 extremos de tabla cerrar paréntesis más fila de tabla con paréntesis abierto con 7 filas con 4 extremos de tabla cerrar paréntesis

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *