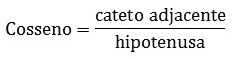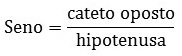Tabla de contenidos
La Ley de los cosenos se utiliza para calcular la medida de un lado o un ángulo desconocido de cualquier triángulo, conociendo sus otras medidas.
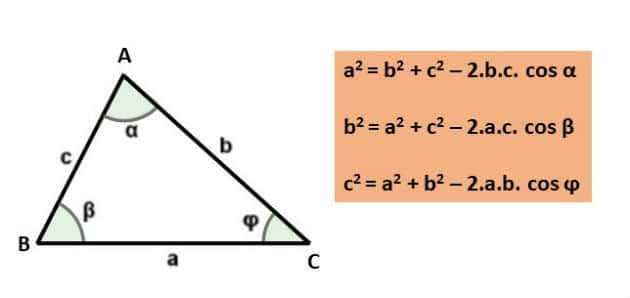
Declaración y fórmulas
El teorema del coseno establece que:
«En cualquier triángulo, el cuadrado de un lado corresponde a la suma de los cuadrados de los otros dos lados, menos el doble del producto de esos dos lados por el coseno del ángulo entre ellos.. «
Así, por la ley de los cosenos tenemos las siguientes relaciones entre los lados y los ángulos de un triángulo:
EJEMPLOS
1. Dos lados de un triángulo miden 20 cm y 12 cm y forman un ángulo de 120º entre ellos. Calcula la medida del tercer lado.
Solución
Para calcular la medida del tercer lado usaremos la ley del coseno. Para esto, consideremos:
b = 20 cm
c = 12 cm
cos α = cos 120º = – 0.5 (valor encontrado en tablas trigonométricas).
Sustituyendo estos valores en la fórmula:
Lados = 20dos + 12dos – dos . 20. 12. (- 0,5)
Lados = 400 + 144 + 240
Lados = 784
a = √784
a = 28 cm
Entonces el tercer lado mide 28 cm.
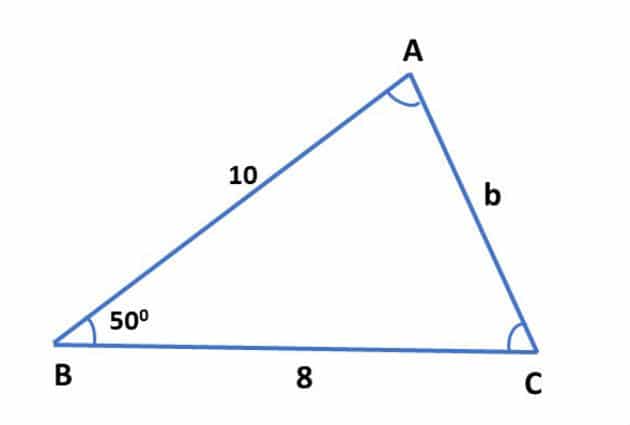
dos. Determine la medida del lado AC y la medida del ángulo del vértice A en la siguiente figura:
Primero, determinemos el AC = b:
Bdos = 8dos + 10dos – dos . 8. 10. cos 50º
Bdos = 164 – 160. cos 50º
Bdos = 164 – 160. 0,64279
b ≈ 7,82
Ahora, determinemos la medida del ángulo por la ley del coseno:
8dos = 10dos + 7,82dos – dos . 10. 7.82. porque
64 = 161,1524 – 156,4 cos Â
cos  = 0,62
 = 52º
Nota: Para encontrar los valores de los ángulos del coseno usamos la Tabla Trigonométrica. En él tenemos los valores de los ángulos del 1º al 90º para cada función trigonométrica (seno, coseno y tangente).
Solicitud
La ley del coseno se puede aplicar a cualquier triángulo. Ya sea en ángulo recto (ángulos internos menores de 90º), ángulo obtuso (con un ángulo interno mayor de 90º), o rectángulo (con un ángulo interno igual a 90º).

¿Y en los Triángulos Rectos?
Apliquemos la ley del coseno al lado opuesto al ángulo de 90º, como se indica a continuación:
Lados = bdos + cdos – dos . B . C . cos 90º
Como cos 90º = 0, la expresión anterior es:
Lados = bdos + cdos
Que es igual a la expresión del Teorema de Pitágoras. Por tanto, podemos decir que este teorema es un caso particular de la ley del coseno.
La ley del coseno es adecuada para problemas en los que conocemos dos lados y el ángulo entre ellos y queremos descubrir el tercer lado.
Aún podemos usarlo cuando conocemos los tres lados del triángulo y queremos conocer uno de sus ángulos.
Para situaciones en las que conocemos dos ángulos y solo un lado y queremos determinar el otro lado, resulta más conveniente utilizar la Ley de Senos.
Definición de coseno y seno
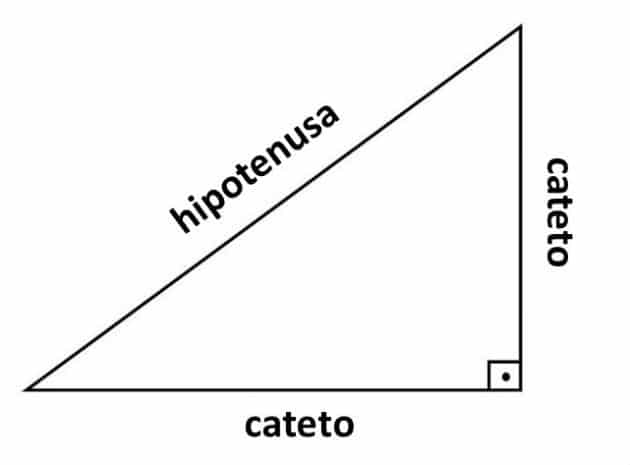
El coseno y el seno de un ángulo se definen como razones trigonométricas en un triángulo rectángulo. El lado opuesto al ángulo recto (90º) se llama hipotenusa y los otros dos lados se llaman colectores, como se muestra en la siguiente figura:
Representación del triángulo rectángulo y sus lados: colateral e hipotenusa
El coseno se define entonces como la relación entre la medida del lado adyacente y la hipotenusa:
El seno, por otro lado, es la relación entre la medida del lado opuesto y la hipotenusa.
Ejercicios
1. Si los lados de un triángulo miden x, x + 1 yx + 2, entonces, para cualquier X real y mayor que 1, el coseno del ángulo interno más grande de este triángulo es igual a:
a) x / x + 1
b) x / x + 2
c) x + 1 / x + 2
d) x – 2 / 3x
e) x – 3 / 2x
dos. (UFRS) En el triángulo representado en la figura siguiente, AB y AC tienen la misma medida, y la altura relativa al lado BC es igual a 2/3 de la medida BC.
Según estos datos, el coseno del ángulo CÂB es:
a) 25/7
b) 7/20
c) 4/5
d) 5/7
e) 5/6
3. Dos lados de un triángulo miden 8 my 10 my forman un ángulo de 60 °. El tercer lado de este triángulo mide:
a) 2√21 m
b) 2√31 m
c) 2√41 m
d) 2√51 m
e) 2√61 m