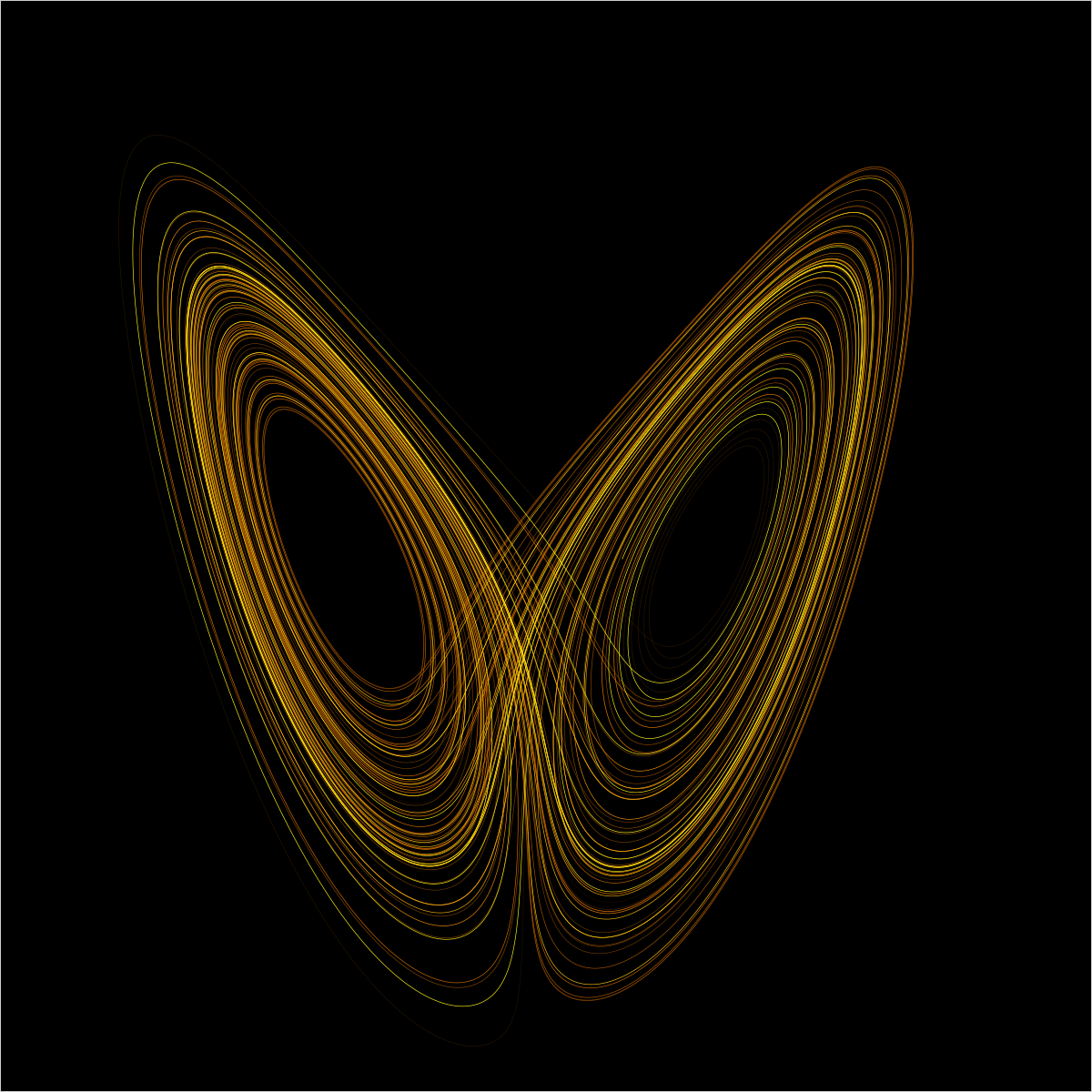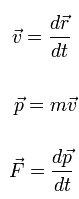Written by admin
Abū ʿAlī al-Ḥusayn ibn ʿAbd Allāh ibn Sīnā, generalmente abreviado ibn Sīnā (procedente de Sīnā (Irán)), latinizado como Avicena (Afshana, actual Uzbekistán c. 980 – Hamadan, Irán, junio de 1037) fue un erudito persa, probablemente el filósofo más importante de la tradición islámica y el filósofo más influyente de la era premoderna. Destacó entre otras […]
Written by admin
Augustin-Louis Cauchy Fue un matemático francés nacido el 21 de agosto de 1789. Fue el matemático que consolidó la matemática moderna contribuyendo al rigor de la matemática moderna sus notaciones. La infancia de Cauchy no fue fácil. Al crecer en medio de la Revolución Francesa, sufrió hambre y necesidad mientras huía al campo debido al […]
Written by admin
(Griego phasis, de phainein, haz que aparezca) Diagrama de fases [1] Ver también en el diccionario: fase MATEMÁTICAS El espacio de fase es un espacio matemático abstracto que permite representar de manera precisa el estado de un sistema dinámico. Para un sistema de dos partículas cuyo movimiento está restringido a una línea, elespacio de fase […]
Written by admin
Teoría que, en su parte elemental, trata de las nociones de conjunto, elemento, subconjunto, álgebra de conjuntos y relaciones y aplicaciones definidas sobre conjuntos, y que, en su parte axiomática, pretende formalizar y axiomatizar la noción intuitiva del todo en para eliminar las paradojas que resultan de ella. (La teoría de conjuntos es la base […]
Written by admin
Máquina de cifrado Enigma Ver también en el diccionario: criptografía Máquina de cifrado EnigmaConjunto de técnicas de cifrado que aseguran la inviolabilidad de los textos y, en informática, de los datos. Principios generales Un sistema de criptografía adopta reglas que definen cómo se cifran o descifran los datos. Se hace una distinción entre técnicas sin […]
Written by admin
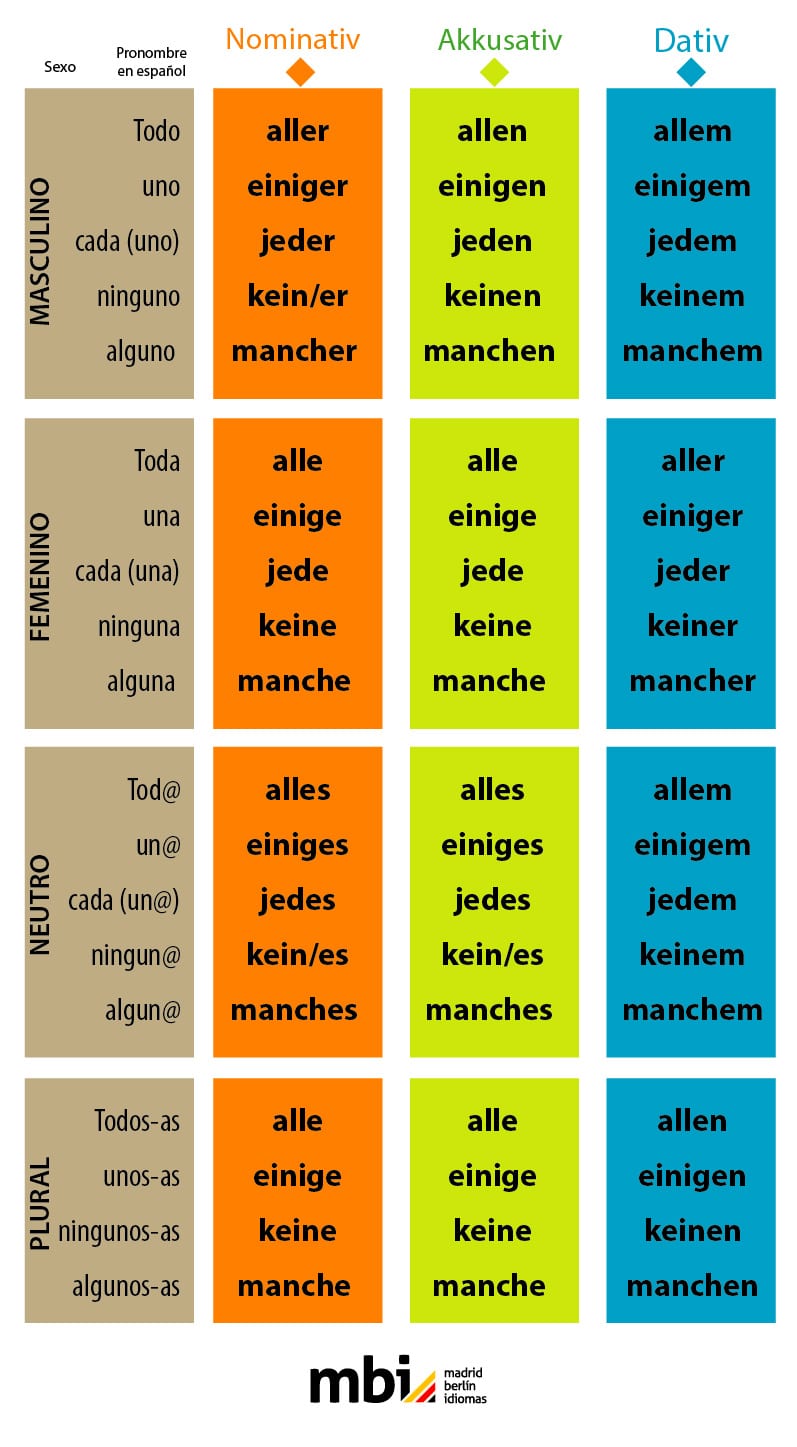
Pronombres indefinidos (pronombre indefinido) generalmente se refieren a un tema de manera inexacta. Suelen utilizarse para la tercera persona, ya sea en singular o en plural. Cuando expresamos una oración como: “Alguien movió mi bolso”, usamos un pronombre indefinido. En este caso, no se explica quién, sino algunas de las personas que lo rodean, ya […]
Written by admin
La ley de acción de masas es un modelo matemático utilizado para describir fenómenos dinámicos en química, como la cinética de las reacciones químicas. La ley dice que la velocidad de una reacción química elemental, es decir, una reacción química que tiene lugar en un solo paso, es proporcional a la concentración de los reactivos. […]
Written by admin
Antes de entender lo que Teoría del caos, es necesario discutir dos términos: determinista y estocástico. El determinista está vinculado al determinismo. Según Gomes (2011): “En epistemología designa la teoría según la cual todo está determinado, es decir, sometido a condiciones necesarias y suficientes, que también están determinadas. Una relación se determina cuando existe un […]
Written by admin
LOS Mecánica newtoniana es una de las tres formulaciones de la mecánica clásica que tienen como objetivo estudiar fenómenos basados en la dinámica de un sistema conservador o no conservador. Su presentación es más simple que la mecánica hamiltoniana y lagrangiana, por lo tanto, tiene un alcance más limitado: la mecánica de Sir Isaac Newton […]
Written by admin
La propiedad de los objetos de caer cuando se sueltan desde una cierta altura del suelo es bien conocida desde la antigüedad. Igualmente conocido fue el movimiento de los cuerpos celestes, observado durante mucho tiempo en una trayectoria circular eterna a través del cielo. Durante gran parte de nuestra historia, ambos movimientos se consideraron naturales, […]
